title: CNN
tags: DL
深度学习以数据的原始形态(raw data)作为算法的输入,经过算法的层层抽象,将原始数据逐层抽象为自身任务所需的最终特种表示,最后以特征到任务的目标的映射(mapping)作为结束,从原始数据到最终任务目标,一气呵成而中间并无夹杂任何人为操作。相比于传统的 ML 算法仅学得模型这一单一任务模块而言,DL 除了模型学习,还有特征学习、特征抽象等任务模块的参与,借助多层任务模块完成最终的学习任务。
神经网络基础概念
神经网络的工作原理
神经网络中每层对输入数据所做的具体操作保存在该层的权重( weight)中,其本质是一串数字。用术语来说,每层实现的变换由其权重来参数化( parameterize)。权重有时也被称为该层的参数( parameter)。在这种语境下,学习的意思是为神经网络的所有层找到一组权重值,使得该网络能够将每个示例输入与其目标正确地一一对应。
一个深度神经网络可能包含数千万个参数。找到所有参数的正确取值可能是一项非常艰巨的任务,特别是考虑到修改某个参数值将会影响其他所有参数的行为。

损失函数(loss function)
想要控制神经网络的输出,就需要能够衡量该输出与预期值之间的距离。这是神经网络损失函数( loss function)的任务,该函数也叫目标函数( objective function)。损失函数的输入是网络预测值与真实目标值(即希望网络输出的结果),然后计算一个距离值,衡量该网络在这个示例上的效果好坏。简而言之,损失函数用于网络如何衡量在训练数据上的性能,即网络如何朝着正确的方向前进。在训练过程中需要将其最小化。它能够衡量当前任务是否已成功完成。

优化器(optimizer)
深度学习的基本技巧是:利用之前的距离值作为反馈信号来对权重值进行微调(fine tuning),以降低当前示例对应的损失值。这种调节由优化器( optimizer)来完成,它实现了所谓的反向传播( backpropagation)算法,这是深度学习的核心算法。其基于训练数据和损失函数来更新网络的机制。决定如何基于损失函数对网络进行更新。它执行的是随机梯度下降( SGD)的某个变体。

神经网络的组件
神经网络的核心组件是层( layer),它是一种数据处理模块,可以将它看成数据 filter 。进去一些数据,出来的数据变得更加有用。具体来说,层从输入数据中提取表示。大多数深度学习都是将简单的层链接起来,从而实现渐进式的数据蒸馏( data distillation)。深度学习模型就像是数据处理的筛子,包含一系列越来越精细的数据 filter (即层)。有些层是无状态的,但大多数的层是有状态的,即层的权重。权重是利用随机梯度下降学到的一个或多个张量,其中包含网络的知识。
神经网络的数据表示
张量的核心在于,它是一个数据容器。它包含的数据几乎总是数值数据,因此它是数字的容器。
张量的关键属性有以下三个关键属性来定义:
- 轴的个数(阶)
- 形状,它是一个整数元祖,表示张量沿每个轴的维度大小(元素大小)
- 数据类型(在Python库中通常叫做
dtype)
梯度
每个神经层都用下述方法对输入数据进行变换。
output = relu(dot(W, input) + b)
W和b都是张量,均为该层的属性。它们被称为该层的权重( weight)或可训练参数( trainable parameter),一开始,这些权重矩阵取较小的随机值,这一步叫作随机初始化( random initialization)。W和b都是随机的,relu(dot(W, input) + b)肯定不会得到任何有用的表示。虽然得到的表示是没有意义的,但这是一个起点。下一步则是根据反馈信号逐渐调节这些权重。这个逐渐调节的过程叫作训练,也就是机器学习中的学习。
上述过程发生在一个训练循环( training loop)内,其具体过程如下(必要时一直重复这些步骤):
- 抽取训练样本
x和对应目标y组成的数据批量 - 在
x上运行网络(这一步叫作前向传播, forward pass),得到预测值y_pred - 计算网络在这批数据上的损失,用于衡量
y_pred和y之间的距离 - 更新网络的所有权重,使网络在这批数据上的损失略微下降
最终得到的网络在训练数据上的损失非常小,即预测值y_pred和预期目标y之间的距离非常小。网络“学会”将输入映射到正确的目标。
计算损失相对于网络系数的梯度( gradient),然后向梯度的反方向改变系数,从而使损失降低。
训练网络
一开始对神经网络的权重随机赋值,因此网络只是实现了一系列随机变换。其输出结果自然也和理想值相去甚远,相应地,损失值也很高。但随着网络处理的示例越来越多,权重值也在向正确的方向逐步微调,损失值也逐渐降低。这就是训练循环( training loop),将这种循环重复足够多的次数(通常对数千个示例进行数十次迭代),得到的权重值可以使损失函数最小。具有最小损失的网络,其输出值与目标值尽可能地接近,这就是训练好的网络。
典型的 Keras 工作流程:
- 定义训练数据:输入张量和目标张量。
- 定义层组成的网络(或模型),将输入映射到目标。
- 配置学习过程:选择损失函数、优化器和需要监控的指标。
- 调用模型的
fit方法在训练数据上进行迭代。
Keras定义模型有两种方法:
- 使用
Sequential类(仅用于层的线性堆叠,这是目前最常见的网络架构) - 函数式
API(functional API,用于层组成的有向无环图,可以构建任意形式的架构)。
为什么需要激活函数?
模型分类:
- 回归模型:预测连续值,是多少的问题。例如,房价是多少?
- 分类模型:预测离散值,是不是的问题。例如,这只动物是不是狗?
卷积层就是我们所做的一大堆特定的滤波器,该滤波器会对某些特定的特征进行强烈的响应,一般情况下是结果值非常大。而对一些无关特性,其响应很小,大部分是结果相对较小,或者几乎为 0。
这样就可以看做为激活,当特定卷积核发现特定特征时,就会做出响应,输出大的数值,而响应函数的存在把输出归为 0~1,那么大的数值就接近 1,小的数值就接近 0。因此在最后计算每种可能所占比重时,自然大的数值比重大。
对于分类问题,画一条直线,这个问题还是比较简单,一条直线解决不了两条就可以了。


这就是一个没有激活函数的网络,可以看出该网络是 x1 和 x2 的线性组合。
线性组合只能是直线

再加一层变为: 。拆开后,结果还是线性的,这样就严重影响了分类的效果,这样根本无法解决非线性问题。
。拆开后,结果还是线性的,这样就严重影响了分类的效果,这样根本无法解决非线性问题。
神经网络的激活函数其实是:将线性转化为非线性的一个函数,并非只是简单地给予 0,或者给予 1。


总而言之,如果不用激活函数,多层神经网络和一层神经网络就没什么区别了。经过多层神经网络的加权计算,都可以展开成一次的加权计算。
交叉熵
刻画了两个概率分布之间的距离,它是分类问题中使用比较广的一种损失函数。给定两个概率分布 p 和 q , 通过 q 来表示 p 的交叉熵为 :

交叉熵刻画的是两个概率分布之间的距离 , 然而神经网络的输出却不一定是一个概率分布。概率分布刻画了不同事件发生的概率。当事件总数有限的情况下 ,概率分布函数  满足 :
满足 :

也就是说,任意事件发生的概率都在 0 和 1 之间,且总有某一个事件发生 (概率的和为 1 )。如果将分类问题中“ 一个样例属于某一个类别”看成一个概率事件,那么训练数据的正确答案就符合一个概率分布。因为事件“一个样例属于不正确的类别”的概率为 1,而“ 一个样例属于正确的类别”的概率为 1 。如何将神经网络前向传播得到的结果也变成概率分布呢? Softmax 回归就是一个非常常用的方法 。
在 TensorFlow 中,Softmax 回归的参数被去掉了,它只是一层额外的处理层,将神经网络的输出变成一个概率分布 。假设原始的神经网络输出为 ,那么经过
,那么经过 Softmax 回归处理之后的输出为 :

从以上公式中可以看出,原始神经网络的输出被用作置信度来生成新的输出,而新的输出满足概率分布的所有要求。这个新的输出可以理解为经过神经网络的推导,一个样例为不同类别的概率分别是多大。这样就把神经网络的输出也变成了一个概率分布,从而可以通过交叉熵来计算预测的概率分布和真实答案的概率分布之间的距离了。
从交叉熵的公式中可以看到,交叉熵函数不是对称( ),它刻画的是通过概率分布
),它刻画的是通过概率分布 q 来表达概率分布 p 的困难程度。因为正确答案是希望得到的结果,所以当交叉熵作为神经网络的损失函数时,p 代表的是正确答案,q 代表的是预测值。交叉熵刻画的是两个概率分布的距离,也就是说交叉熵值越小,两个概率分布越接近。
全连接层的作用
- 全连接层(fully connected layers,FC)在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。在实际使用中,全连接层可由卷积操作实现:对前层是全连接的全连接层可以转化为卷积核为
1x1的卷积;而前层是卷积层的全连接层可以转化为卷积核为hxw的全局卷积,h和w分别为前层卷积结果的高和宽。 - 目前由于全连接层参数冗余(仅全连接层参数就可占整个网络参数
80%左右),近期一些性能优异的网络模型如 ResNet 和 GoogLeNet 等均用全局平均池化(global average pooling,GAP)取代 FC 来融合学到的深度特征,最后仍用 softmax 等损失函数作为网络目标函数来指导学习过程。需要指出的是,用 GAP 替代 FC 的网络通常有较好的预测性能。 - 在 FC 越来越不被看好的当下,我们近期的研究(In Defense of Fully Connected Layers in Visual Representation Transfer)发现,FC 可在模型表示能力迁移过程中充当“防火墙”的作用。具体来讲,假设在 ImageNet 上预训练得到的模型为
,则 ImageNet 可视为源域(迁移学习中的 source domain)。微调(fine tuning)是深度学习领域最常用的迁移学习技术。针对微调,若目标域(target domain)中的图像与源域中图像差异巨大(如相比 ImageNet,目标域图像不是物体为中心的图像,而是风景照,见下图),不含 FC 的网络微调后的结果要差于含 FC 的网络。因此,FC 可视作模型表示能力的“防火墙”,特别是在源域与目标域差异较大的情况下,FC 可保持较大的模型 capacity 从而保证模型表示能力的迁移(冗余的参数并不一无是处)。


【注】 有关卷积操作“实现”全连接层,需要注意:以 VGG-16 为例,对 224x224x3 的输入,最后一层卷积可得输出为 7x7x512,如后层是一层含 4096 个神经元的 FC,则可用卷积核为 7x7x512x4096 的全局卷积来实现这一全连接运算过程,其中该卷积核参数如下:
filter_size = 7,
padding = 0,
stride = 1,
D_in = 512,
D_out = 4096
经过此卷积操作后可得输出为 1x1x4096。如需再次叠加一个 2048 的 FC,则可设定卷积层操作参数为:
filter_size = 1,
padding = 0,
stride = 1,
D_in = 4096,
D_out = 2048
Dropout
1. Dropout 出现的缘由
在机器学习的模型中,如果模型的参数太多,而训练样本又太少,训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题,过拟合具体表现在:模型在训练数据上损失函数较小,预测准确率较高;但是在测试数据上损失函数比较大,预测准确率较低。
过拟合是很多机器学习的通病。如果模型过拟合,那么得到的模型几乎不能用。为了解决过拟合问题,一般会采用模型集成的方法,即训练多个模型进行组合。此时,训练模型费时就成为一个很大的问题,不仅训练多个模型费时,测试多个模型也是很费时。
总而言之,训练深度神经网络的时候,总是会遇到两大缺点:
- 容易过拟合
- 费时
Dropout 可以比较有效的缓解过拟合的发生,在一定程度上达到正则化的效果。
2. Dropout 的概念
在 2012 年,Hinton 在其论文《Improving neural networks by preventing co-adaptation of feature detectors》中提出 Dropout。当一个复杂的前馈神经网络被训练在小的数据集时,容易造成过拟合。为了防止过拟合,可以通过阻止特征检测器的共同作用来提高神经网络的性能。
Dropout 可以作为训练深度神经网络的一种 trick 供选择。在每个训练批次中,通过忽略一半的特征检测器(让一半的隐层节点值为 0),可以明显地减少过拟合现象。这种方式可以减少特征检测器(隐层节点)间的相互作用,检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。
简而言之,Dropout 就是在前向传播的时候,让某个神经元的激活值以一定的概率 p 停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征,如下图所示。

3. Dropout 具体工作流程
假设要训练这样一个神经网络:

输入是 x,输出是 y,正常的流程是:首先把 x 通过网络前向传播,然后把误差反向传播以决定如何更新参数让网络进行学习。使用 Dropout 之后,过程变成如下:
首先随机(临时)删掉网络中一半的隐藏神经元,输入输出神经元保持不变(下图中虚线为部分临时被删除的神经元)

然后把输入
x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后,在没有被删除的神经元上按照随机梯度下降法更新对应的参数(w, b)。然后继续重复以下过程:
恢复被删掉的神经元(此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
从隐藏层神经元中随机选择一个一半大小的子集临时删除掉(备份被删除神经元的参数)。
对一小批训练样本,先前向传播然后反向传播损失并根据随机梯度下降法更新参数
(w, b)(没有被删除的那一部分参数得到更新,删除的神经元参数保持被删除前的结果)。
不断重复这一过程。
4. Dropout 的使用
Dropout 具体怎么让某些神经元以一定的概率停止工作(就是被删除掉)?代码层面如何实现呢?
Dropout 代码层面的一些公式推导及代码实现思路。
1. 在训练模型阶段
无可避免的,在训练网络的每个单元都要添加一个概率流程。

现在描述 dropout 神经网络模型,其中有 L 层隐藏层,隐藏层索引为 。
。 表示第
表示第 层隐藏层的输入向量,
层隐藏层的输入向量,  表示第
表示第 层隐藏层的输出向量(
层隐藏层的输出向量( 表示输入)。
表示输入)。 和
和 分别表示第
分别表示第 层隐藏层的权重与偏置值,
层隐藏层的权重与偏置值, 表示激活函数。
表示激活函数。
对应的公式变化如下:
没有
Dropout的网络计算公式:
采用
Dropout的网络计算公式:
上面公式中,Bernoulli 函数是为了生成概率
r向量,也就是随机生成一个0、1的向量。
代码层面实现让某个神经元以概率 p 停止工作,其实就是让它的激活函数值的从概率 p 变为 0。比如某一层网络神经元的个数为 1000 个,其激活函数输出值为 y1、y2、y3、...、y1000,dropout比率选择 0.4,那么这一层神经元经过 dropout 后,1000 个神经元中会有大约 400 个的值被置为 0。
注意: 经过上面屏蔽掉某些神经元,使其激活值为 0 以后,还需要对向量 y1、y2、y3、...、y1000 进行缩放,也就是乘以 1/(1-p)。如果在训练的时候,经过置 0 后,没有对 y1、y2、y3、...、y1000 进行缩放(rescale),那么在测试的时候,就需要对权重进行缩放,操作如下。
2. 在测试模型阶段
预测模型的时候,每一个神经单元的权重参数要乘以概率 p。

测试阶段 dropout 公式:

5. 为什么Dropout 可以解决过拟合?
- 取平均的作用: 先回到标准的模型(即没有
dropout),用相同的训练数据去训练5个不同的神经网络,一般会得到5个不同的结果,此时可以采用 “5个结果取均值”或者“多数取胜的投票策略“去决定最终结果。例如,3个网络判断结果为数字9,那么很有可能真正的结果就是数字9,其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合,取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络,随机删掉一半隐藏神经元导致网络结构已经不同,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。 - 减少神经元之间复杂的共适应关系: 因为
dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ,这些特征在其它的神经元的随机子集中也存在。换句话说,假如神经网络是在做出某种预测,它不应该对一些特定的线索片段太过敏感,即使丢失特定的线索,它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1,L2正则,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
6. Dropout 在 Keras 中的源码分析
def dropout(x, level, noise_shape=None, seed=None):
"""Sets entries in `x` to zero at random,
while scaling the entire tensor.
# Arguments
x: tensor
level: fraction of the entries in the tensor
that will be set to 0.
noise_shape: shape for randomly generated keep/drop flags,
must be broadcastable to the shape of `x`
seed: random seed to ensure determinism.
"""
if level < 0. or level >= 1:
raise ValueError('Dropout level must be in interval [0, 1[.')
if seed is None:
seed = np.random.randint(1, 10e6)
if isinstance(noise_shape, list):
noise_shape = tuple(noise_shape)
rng = RandomStreams(seed=seed)
retain_prob = 1. - level
if noise_shape is None:
random_tensor = rng.binomial(x.shape, p=retain_prob, dtype=x.dtype)
else:
random_tensor = rng.binomial(noise_shape, p=retain_prob, dtype=x.dtype)
random_tensor = T.patternbroadcast(random_tensor,
[dim == 1 for dim in noise_shape])
x *= random_tensor
x /= retain_prob
return x
对 Keras 中 dropout 实现函数做一些修改,让 dropout 函数可以单独运行(函数中,x 是本层网络的激活值,level 就是 dropout 每个神经元要被丢弃的概率)。
import numpy as np
# dropout函数的实现
def dropout(x, level):
#level是概率值,必须在0~1之间
if level < 0. or level >= 1:
raise ValueError('Dropout level must be in interval [0, 1[.')
retain_prob = 1. - level
# 通过binomial函数,生成与x一样的维数向量。binomial函数就像抛硬币一样,可以把每个神经元当做抛硬币一样
# 硬币 正面的概率为p,n表示每个神经元试验的次数
# 因为每个神经元只需要抛一次就可以了,所以n=1,size参数是有多少个硬币。
random_tensor = np.random.binomial(n=1, p=retain_prob, size=x.shape) #即将生成一个0、1分布的向量,0表示这个神经元被屏蔽,不工作了,也就是dropout了
print(random_tensor)
x *= random_tensor
print(x)
x /= retain_prob
return x
#对dropout的测试,大家可以跑一下上面的函数,了解一个输入x向量,经过dropout的结果
x=np.asarray([1,2,3,4,5,6,7,8,9,10],dtype=np.float32)
dropout(x,0.4)
# [1 0 0 0 0 1 1 1 1 0]
# [1. 0. 0. 0. 0. 6. 7. 8. 9. 0.]
# [1 1 1 0 1 1 1 0 0 1]
# [ 1. 2. 3. 0. 5. 6. 7. 0. 0. 10.]
注意: Keras 中 dropout 的实现,是屏蔽掉某些神经元,使其激活值为 0 以后,对激活值向量 x1、...、x1000 进行放大,也就是乘以 1/(1-p)。
在训练的时候会随机的丢弃一些神经元,但是预测的时候就没办法随机丢弃了。如果丢弃一些神经元,这会带来结果不稳定的问题,也就是给定一个测试数据,有时候输出 a ,有时候输出 b,结果不稳定,这是实际系统不能接受的,用户可能认为模型预测不准。那么一种”补偿“的方案就是每个神经元的权重都乘以一个 p,这样在“总体上”使得测试数据和训练数据是大致一样的。比如一个神经元的输出是 x,那么在训练的时候它有 p 的概率参与训练,(1-p) 的概率丢弃,那么它输出的期望是 px+(1-p)0=px。因此,测试的时候把这个神经元的权重乘以 p 可以得到同样的期望。
基础知识
无监督预训练(Unsupervised pre-training)
指预训练阶段的样本不需要人工标注数据
有监督预训练(Supervised pre-training)
也可以将其称为迁移学习。简而言之,就是把一个训练好的参数,拿到另外一个任务上,作为神经网络的初始参数值,这样就比直接采用随机初始化的方法的精度要提升很多。
例如,比如已经有一大堆标注好的人脸年龄分类的图片数据,训练了一个CNN,用于人脸的年龄识别。然后,当新的项目任务是:人脸性别识别时,便可以直接利用已经训练好的年龄识别CNN模型,去掉最后一层,然后其它的网络层参数就直接复制过来,继续进行训练。
Ground Truth
机器学习包括有监督学习(supervised learning),无监督学习(unsupervised learning),和半监督学习(semi-supervised learning)。
在有监督学习中,数据是有标注的,以 (x, t) 的形式出现,其中 x 是输入数据,t 是标注。正确的 t 标注是 ground truth, 错误的标记则不是。(也有人将所有标注数据都叫做 ground truth)
由模型函数的数据则是由 (x, y) 的形式出现的。其中 x 为之前的输入数据,y 为模型预测的值。标注会和模型预测的结果作比较。在损耗函数(loss function / error function)中会将 y 和 t 作比较,从而计算损耗(loss / error)。 比如在最小方差中:

因此,如果标注数据不是 ground truth,那么 loss 的计算将会产生误差,从而影响到模型质量。
例子:(比如输入三维,判断是否性感)
1. 错误的数据
- 标注数据
1:((84,62,86), 1),其中x = (84,62,86),t = 1 - 标注数据
2:((84,162,86), 1),其中x = (84,162,86),t = 1
这里标注数据 1 是 ground truth, 而标注数据 2 不是。
- 预测数据
1:y = -1 - 预测数据
2:y = -1

2. 正确的数据
- 标注数据
1:((84,62,86) ,1),其中x =(84,62,86),t = 1 - 标注数据
2:((84,162,86) ,1),其中x =(84,162,86),t = -1(改为 ground truth)
这里标注数据 1 和 2 都是 ground truth。
- 预测数据
1:y = -1 - 预测数据
2:y = -1
总之一句话:ground truth 就是标定好的真实数据。
模型参数(model parameter)& 模型超参数(model Hyperparameter)
1. 模型参数
模型是模型内部的配置变量,其值可以根据数据进行估计。其属性为:
- 模型在进行预测时需要它们
- 它们的值定义了可使用的模型
- 它们是从数据估计或获悉的
- 它们通常不由编程者手动设置
- 它们通常被保存为学习模型的一部分
参数是机器学习算法的关键,它们通常由过去的训练数据中总结得出。
在经典的机器学习文献中,可以将模型看作假设,将参数视为对特定数据集的量身打造的假设。最优化算法是估计模型参数的有效工具。
- 统计:在统计学中,您可以假设一个变量的分布,如高斯分布。高斯分布的两个参数是平均值(
\μ)和标准偏差(\sigma)。这适用于机器学习,其中这些参数可以从数据中估算出来并用作预测模型的一部分。 - 编程:在编程中,可以将参数传递给函数。在这种情况下,参数是一个函数参数,它可能具有一个值范围之一。在机器学习中,在使用的特定模型是函数时,需要参数才能对新数据进行预测。
模型是否具有固定或可变数量的参数决定了它是否可以被称为“参数”或“非参数”。模型参数的一些示例包括:
- 神经网络中的权重
- 支持向量机中的支持向量
- 线性回归或逻辑回归中的系数
2. 模型超参数
模型超参数是模型外部的配置,其值无法从数据中估计。其性质为:
- 它们通常用于帮助估计模型参数。
- 它们通常由人工指定。
- 它们通常可以使用启发式设置。
- 它们经常被调整为给定的预测建模问题。
虽然无法知道给定问题的模型超参数的最佳值,但可以使用经验法则,在其他问题上使用复制值,或通过反复试验来搜索最佳值。
如果模型超参数被称为模型参数,会造成很多混淆。克服这种困惑的一个经验法则为:如果必须手动指定模型参数,那么它可能是一个模型超参数。
模型超参数的一些例子包括:
- 训练神经网络的学习速率。
- 用于支持向量机的
C和\sigma超参数。 K最近邻的K。
总之,模型参数是根据数据自动估算的。但模型超参数是手动设置的,并且在过程中用于帮助估计模型参数。
top-1 & top-5
ImageNet 图像分类大赛评价标准采用 top-5 错误率,或者top-1错误率,即对一张图像预测5个类别,只要有一个和人工标注类别相同就算对,否则算错。
Top-1 = (正确标记 与 模型输出的最佳标记不同的样本数)/ 总样本数Top-5 = (正确标记 不在 模型输出的前5个最佳标记中的样本数)/ 总样本数
top1 就是你所预测的 label 取最后概率向量里面最大的那一个作为预测结果,如果你的预测结果中概率最大的那个分类正确,则预测正确;否则预测错误。top5 就是最后概率向量最大的前五名中,只要出现了正确概率即为预测正确。否则预测错误。
简而言之,ImageNet 图像通常有 1000 个可能的类别,对每幅图像你可以猜 5 次结果(即同时预测 5 个类别标签),当其中有任何一次预测对了,结果都算对,当 5 次全都错了的时候,才算预测错误,这时候的分类错误率就叫 top5 错误率。同理,top-k 就是对应于有 k 次机会可以进行预测。
epoch
- iteration:表示
1次迭代(也叫 training step),每次迭代更新1次网络结构的参数(batch-size 个训练数据forward+backward后更新参数过程。) - batch-size:
1次迭代所使用的样本量 - epoch:
1个 epoch 表示过了1遍训练集中的所有样本(所有训练数据forward+backward后更新参数的过程)
具体计算公式为:
one epoch = numbers of iterations = N = 训练样本的数量 / batch_size
值得注意的是,在深度学习领域中,常用带 mini-batch 的随机梯度下降算法(Stochastic Gradient Descent, SGD)训练深层结构,它有一个好处就是并不需要遍历全部的样本,当数据量非常大时十分有效。此时,可根据实际问题来定义 epoch,例如定义 10000 次迭代为 1 个 epoch,若每次迭代的 batch-size 设为 256,那么 1 个 epoch 相当于过了 2560000 个训练样本。
感受野(receptive field)
定义
在卷积神经网络 CNN 中,决定某一层输出结果中一个元素所对应的输入层的区域大小,被称作感受野。这段定义非常简单,用数学的语言就是感受野是 CNN 中的某一层输出结果的一个元素对应输入层的一个映射。再通俗点的解释是,feature map 上的一个点对应输入图上的区域【注意:这里是输入图,不是原始图。好多博客写的都是原图上的区域,经过一番的资料查找,发现并不是原图】。
感受野表示输入空间中一个特定 CNN 特征的范围区域(The receptive field is defined as the region in the input space that a particular CNN’s feature is looking at)。一个特征的感受野可以采用区域的中心位置和特征大小进行描述。
目前流行的物体识别方法都是围绕感受野来做的设计,就如 SSD 和 Faster RCNN。理解好感受野的本质有两个好处:
- 理解卷积的本质
- 更好的理解 CNN 的整个架构。
感受野的计算和可视化
CNN特征图可视化的两种方式:

如上图所示,采用卷积核 C 的核大小 ksize=3x3,填充大小 padding=1x1,步长 stride=2x2。(图中上面一行)对 5x5 的输入特征图进行卷积生成 3x3 的绿色特征图。(图中下面一行)对上面绿色的特征图采用相同的卷积操作生成 2x2 的橙色特征图(图中左边一列)按列可视化 CNN 特征图,如果只看特征图,我们无法得知特征的位置(即感受野的中心位置)和区域大小(即感受野的大小),而且无法深入了解 CNN 中的感受野信息。(图中右边一列)CNN 特征图的大小固定,其特征位置即感受野的中心位置。
说的有点晦涩难懂,应该是学术的讲法,简洁的理解就是,左图是常规的卷积过程。而对于右图,卷积后的图像和原图一样大,这个操作起来并不难,就是各个特征(可以理解为图像中的像素点)的位置在卷积后保持不变,空的部分用空白来填充。这样做有什么好处,在我们后面会说到。只要注意到,左图和右图在卷积后,其特征的数目(绿色和黄色点的数目)是一样的。

上图的信息量很大,内容很多,有 CNN 的卷积过程,有感受野的计算公式和过程。弄懂了上图就知道感受野到底是个怎么回事了。
还记得感受野的定义吗?具体看 layer 1 的 feature map 左上角带有红点的特征(可以理解为一个像素),它对应输入 layer 0 的区域大小就是我们要计算的感受野。
很显然,经过 3x3 卷积核卷积后,它对应 layer 0 层上的灰色区域(别忘了还有 padding)。再看 layer 1 到 layer 2 的过程,卷积过程的第一步是先加 padding,p2=1,这里的 1 是特征所占的区域,换句话说就是一个特征所占的感受野。所以 Conv2 过程这张图才会在外面加上了三个格。s2=2 也是同样的道理,步长也是跨过两个特征。k2=3 也是如此,包含 3x3 个特征。经过卷积后就来到了 layer 2 了,左上角特征的感受野大小也很明显了,就是灰色部分。它这一个点可要完成接下来组织交代的历史任务。
这整个过程下来,是不是明白点意思了。感受野的计算有卷积逆过程的意思,这里我不能给出直接的定义,因为还没有权威这么说。之前讲了,明白了感受野的计算能更好理解卷积过程对吧。从上图我们再琢磨一下。特征图的大小逐渐变小,一个特征表示的信息量越来越大,这不就是有点压缩的意思嘛。将原图感兴趣的信息提取出来,不关注的统统抛掉。提的过程就是 CNN 的前向传播,抛的过程就是 CNN 的反馈学习。
上图展示了一些感受野的例子,采用核大小核大小 ksize=3x3,填充大小 padding=1x1,步长 stride=2x2 的卷积核 C 对 5x5 大小的输入图进行卷积操作,将输出 3x3 大小的特征图(绿色图)。对 3x3 大小的特征图进行相同的卷积操作,将输出 2x2 的特征图(橙色)。输出特征图在每个维度上的大小可以采用下面的公式进行计算:

为了简单,假设 CNN 的架构是对称的,而且输入图像长宽比为 1,因此所有维度上的变量值都相同。若 CNN 架构或者输入图像不是对称的,你也可以分别计算每个维度上的特征图大小。如上图所示,左边一列展示了一种 CNN 特征图的常见可视化方式。这种可视化方式能够获取特征图的个数,但无法计算特征的位置(感受野的中心位置)和区域大小(感受野尺寸)。上图右边一列展示了一种固定大小的 CNN 特征图可视化方式,通过保持所有特征图大小和输入图大小相同来解决上述问题,接下来每个特征位于其感受野的中心。由于特征图中所有特征的感受野尺寸相同,我们就可以非常方便画出特征对应的 bounding box 来表示感受野的大小。因为特征图大小和输入图像相同,所以我们无需将包围盒映射到输入层。

另外一种固定大小的 CNN 特征图表示。采用相同的卷积核 C 对 7x7 大小的输入图进行卷积操作,这里在特征中心周围画出了感受野的 bounding box。为了表达更清楚,这里忽略了周围的填充像素。固定尺寸的 CNN 特征图可以采用 3D(左图)或 2D(右图)进行表示。
上图展示了另外一个例子,采用相同的卷积核 C 对 7x7 大小的输入图进行卷积操作。这里给出了 3D(左图)和 2D(右图)表示下的固定尺寸 CNN 特征图。注意:上图中感受野尺寸逐渐扩大,第二个特征层的中心特征感受野很快就会覆盖整个输入图。这一点对于 CNN 设计架构的性能提升非常重要。
感受野的计算(Receptive Field Arithmetic)
除了每个维度上特征图的个数,还需要计算每一层的感受野大小,因此我们需要了解每一层的额外信息,包括:当前感受野的尺寸 r,相邻特征之间的距离(或者jump)j,左上角(起始)特征的中心坐标 start,其中特征的中心坐标定义为其感受野的中心坐标(如上述固定大小 CNN 特征图所述)。假设卷积核大小 k,填充大小 p,步长大小 s,则其输出层的相关属性计算如下:

- 公式一基于输入特征个数和卷积相关属性计算输出特征的个数
- 公式二计算输出特征图的
jump,等于输入图的jump与输入特征个数(执行卷积操作时jump的个数,stride 的大小)的乘积 - 公式三计算输出特征图的 receptive field size,等于
k个输入特征覆盖区域加上边界上输入特征的感受野覆盖的附加区域
- 公式四计算第一个输出特征的感受野的中心位置,等于第一个输入特征的中心位置,加上第一个输入特征位置到第一个卷积核中心位置的距离
,再减去填充区域大小
。注意:这里都需要乘上输入特征图的
jump,从而获取实际距离或间隔。
例子
用于计算给定 CNN 架构下所有层的感受野信息。程序允许输入任何特征图的名称和图中特征的索引号,输出相关感受野的尺寸和位置。

AlexNet 下感受野计算样例:
# [filter size, stride, padding]
#Assume the two dimensions are the same
#Each kernel requires the following parameters:
# - k_i: kernel size
# - s_i: stride
# - p_i: padding (if padding is uneven, right padding will higher than left padding; "SAME" option in tensorflow)
#
#Each layer i requires the following parameters to be fully represented:
# - n_i: number of feature (data layer has n_1 = imagesize )
# - j_i: distance (projected to image pixel distance) between center of two adjacent features
# - r_i: receptive field of a feature in layer i
# - start_i: position of the first feature's receptive field in layer i (idx start from 0, negative means the center fall into padding)
import math
convnet = [[11,4,0],[3,2,0],[5,1,2],[3,2,0],[3,1,1],[3,1,1],[3,1,1],[3,2,0],[6,1,0], [1, 1, 0]]
layer_names = ['conv1','pool1','conv2','pool2','conv3','conv4','conv5','pool5','fc6-conv', 'fc7-conv']
imsize = 227
def outFromIn(conv, layerIn):
n_in = layerIn[0]
j_in = layerIn[1]
r_in = layerIn[2]
start_in = layerIn[3]
k = conv[0]
s = conv[1]
p = conv[2]
n_out = math.floor((n_in - k + 2*p)/s) + 1
actualP = (n_out-1)*s - n_in + k
pR = math.ceil(actualP/2)
pL = math.floor(actualP/2)
j_out = j_in * s
r_out = r_in + (k - 1)*j_in
start_out = start_in + ((k-1)/2 - pL)*j_in
return n_out, j_out, r_out, start_out
def printLayer(layer, layer_name):
print(layer_name + ":")
print("\t n features: %s \n \t jump: %s \n \t receptive size: %s \t start: %s " % (layer[0], layer[1], layer[2], layer[3]))
layerInfos = []
if __name__ == '__main__':
#first layer is the data layer (image) with n_0 = image size; j_0 = 1; r_0 = 1; and start_0 = 0.5
print ("-------Net summary------")
currentLayer = [imsize, 1, 1, 0.5]
printLayer(currentLayer, "input image")
for i in range(len(convnet)):
currentLayer = outFromIn(convnet[i], currentLayer)
layerInfos.append(currentLayer)
printLayer(currentLayer, layer_names[i])
print ("------------------------")
layer_name = raw_input ("Layer name where the feature in: ")
layer_idx = layer_names.index(layer_name)
idx_x = int(raw_input ("index of the feature in x dimension (from 0)"))
idx_y = int(raw_input ("index of the feature in y dimension (from 0)"))
n = layerInfos[layer_idx][0]
j = layerInfos[layer_idx][1]
r = layerInfos[layer_idx][2]
start = layerInfos[layer_idx][3]
assert(idx_x < n)
assert(idx_y < n)
print ("receptive field: (%s, %s)" % (r, r))
个人聚德计算计算感受野的作用是可以帮助设计网络结构,至少可以大事了解到在每一层的特征所涵盖的信息量。例如,输入图像大小是 250x250的 情况下,如果最后一层的感受野能超过 250 的话,那么可以认为在做最后的分类判断时所用到的特征已经涵盖了原始图像所有范围的信息了。在保证最后一层特征的感受野大小的情况下,如果能够尽可能的降低网络的参数总量,那么就是件很有意义的事情。事实上 inception model 就是这样的思路,通过非对称的结构来降低参数量,同时还能保证感受野。
IoU
物体检测需要定位出物体的 bounding box。如下图所示,不仅要定位出车辆的 bounding box,还需要识别出 bounding box里面的物体就是车辆。对于 bounding box 的定位精度,存在一个定位精度评价公式:IoU(因为算法不可能百分百跟人工标注的数据完全匹配)。

IoU定义了两个 bounding box 的重叠度:

矩形框 A、B的一个重合度 IoU 计算公式为:

即,矩形框 A、B 的重叠面积占 A、B并集的面积比例:

非极大值抑制
非极大值抑制(NMS)就是:抑制不是极大值的元素,搜索局部的极大值。这个局部代表的是一个邻域,邻域有两个参数可变,一是邻域的维数,二是邻域的大小。
【注】:此处不讨论通用的 NMS 算法,而是应用于目标检测中用于提取分数最高的窗口。例如,在行人检测中,滑动窗口经提取特征,经分类器分类识别后,每个窗口都会得到一个分数。但滑动窗口会导致很多窗口与其他窗口存在包含或者大部分交叉的情况。这时就需要用到NMS来选取那些邻域里分数最高(即,行人的概率最大),并且抑制那些分数低的窗口。
RCNN 算法会从一张图片中找出 n 多个可能是物体的矩形框,然后为每个矩形框分别作类别分类概率。
如下图所示,定位一个车辆,最后算法找出了一堆方框,需要判别哪些矩形框是没用的。非极大值抑制法的步骤:先假设有6个矩形框,根据分类器类别分类概率做排序,从小到大分别属于车辆的概率分别为A、B、C、D、E、F:
- 从最大概率矩形框
F开始,分别判断A~E与F的重叠度IoU是否大于某个设定的阈值。 - 假设
B、D与F的重叠度超过阈值,则扔掉B、D,并标记第一个矩形框F是要保留下来的。 - 从剩下的矩形框
A、C、E中,选择概率最大的E,然后判断E与A、C的重叠度IoU,重叠度大于一定的阈值就扔掉;并标记E是保留下来的第二个矩形框。
一直重复,找到所有被保留下来的矩形框。

对梯度幅值进行非极大值抑制
图像梯度幅值矩阵中的元素值越大,说明图像中该点的梯度值越大,但这不不能说明该点就是边缘(这仅仅是属于图像增强的过程)。在 Canny 算法中,非极大值抑制是进行边缘检测的重要步骤,通俗意义上是指:寻找像素点局部最大值,将非极大值点所对应的灰度值置为0,这样可以剔除掉一大部分非边缘的点。

非极大值抑制的工作原理:
由上图可知,要进行非极大值抑制,首先要确定像素点 C 的灰度值在其八邻域内是否为最大。蓝色线条方向为 C 点的梯度方向(这样就可以确定其局部的最大值肯定分布在这条线上),即除了 C 点外,梯度方向的交点 dTmp1 和 dTmp2 这两个点的值也可能会是局部最大值。
因此,判断 C 点灰度与这两个点灰度大小,即可判断 C 点是否为其邻域内的局部最大灰度点。如果经过判断,C 点灰度值小于这两个点中的任一个,那就说明 C 点不是局部极大值,那么则可以排除 C 点为边缘。
在实际中,其实只能得到 C 点邻域的 8 个点的值,而 dTmp1 和 dTmp2 并不在其中。要得到这两个值,就需要对该两个点两端的已知灰度进行线性插值,即根据上图中的 g1 和 g2 对 dTmp1 进行插值,根据 g3 和 g4 对 dTmp2 进行插值,这要用到其梯度方向。
完成非极大值抑制后,会得到一个二值图像,非边缘的点灰度值均为 0,可能为边缘的局部灰度极大值点可设置其灰度为 128。
物体检测 VS 图片分类
物体检测和图片分类的区别:
- 图片分类不需要定位,而物体检测需要定位出物体的位置,也就是相当于把物体的 bbox 检测出来。
- 物体检测是要把所有图片中的物体都识别定位出来。
简言之,物体检测需要定位出物体的位置,这种就相当于回归问题,求解一个包含物体的方框。而图片分类其实是逻辑回归。这种方法对于单物体检测还不错,但是对于多物体检测便显得捉襟见肘。
Selective Search for Object Recognition
目标检测 VS 目标识别
- 目标识别(object recognition)是指明一幅输入图像中存在哪些对象(目标)。它将整张图像作为输入,输出的是该图像中存在的对象(目标)的类标签(class labels)和类概率(class probability)。例如,类标签为“狗”,相关的类概率是
97%。 - 目标检测(object detection)不仅要告诉输入图像中包含了哪类目标,还要框出该目标的具体位置—利用 bounding boxes
(x, y, width, height)来指示图像内对象的位置。

所有的目标检测算法的核心是目标识别算法。在目标检测时,为了定位到目标的具体位置,通常会把图像分成许多子块(sub-regions / patches),然后把子块作为输入,送到目标识别的模型中。生成较小区域最直接方法叫滑动窗口法(Sliding Window Algorithm)。滑动窗口的方法就是按照子块的大小在整幅图像上穷举所有子图像块。这种方法产生的数据量想想都头大。和滑动窗口法相对的是另外一类基于区域(Region Proposal Algorithms)的方法,例如 selective search。
Sliding Window Algorithm
在滑动窗口方法中,在图像上滑动框或窗口以选择 patch,并使用对象识别(object recognition)模型对窗口覆盖的每个图像 patch 进行分类。 它对整个图像上的对象进行详尽搜索:不仅需要搜索图像中的所有可能位置,还必须以不同的比例进行搜索(这是因为物体识别模型通常以特定尺度(或尺度范围)训练)。
滑窗法的物体检测流程图:

通过滑窗法的主要思路:首先对输入图像进行不同窗口大小的滑窗进行从左往右、从上到下的滑动。每次滑动时候,对当前窗口执行分类器(分类器是事先训练好的)。如果当前窗口得到较高的分类概率,则认为检测到了物体。对每个不同窗口大小的滑窗都进行检测后,会得到不同窗口检测到的物体标记,这些窗口大小会存在重复较高的部分,最后采用NMS进行筛选。最终,经过NMS筛选后获得检测到的物体。
滑窗法简单易于理解,但是不同窗口大小进行图像全局搜索导致效率低下,而且设计窗口大小时候还需要考虑物体的长宽比。所以,对于实时性要求较高的分类器,不推荐使用滑窗法。
滑动窗口方法适用于固定宽高比的物体,例如面部或行人。由于图像是3D对象的2D投影,所以宽高比和形状等对象特征会因为拍摄图像的角度而有很大差异。由于滑动窗口方法需要搜索多个宽高比,所以计算将十分耗时。
Region Proposal Algorithms
这种方法将图像作为输入,将输出边 bounding boxes —其对应于图像中最有可能为对象的所有patches。这些区域提议(region proposals)可能是嘈杂的(noisy)、重叠的(overlapping),并且可能没有完全包含对象。但是在这些区域提议中,将有一个非常接近图像中的实际对象的提议(proposal)。然后,可以使用目标识别模型对这些提议进行分类,具有高概率分数的区域提议是对象的位置。
区域提议算法使用分段(segmentation)识别图像中的预期对象。在分割中,基于一些标准(例如颜色,纹理等)将相邻区域进行分组。与在所有像素位置和所有尺度上寻找对象的 sliding window approach 不同,region proposal algorithm 通过以下方式工作:将像素分成为较少数量的段(segments)。因此,生成的最终提案数量比滑动窗口方法少很多倍。这就减少了必须分类的图像 patches 的数量,这些生成的区域提议具有不同的比例和宽高比。
Selective Search
选择搜索算法的主要观点:图像中物体可能存在的区域应该是有某些相似性或者连续性区域的。因此,选择搜索基于上面这一想法采用子区域合并的方法进行提取 bounding boxes 候选边界框。首先,对输入图像进行分割算法产生许多小的子区域。其次,根据这些子区域之间相似性(相似性标准主要有颜色、纹理、大小等等)进行区域合并,不断的进行区域迭代合并。每次迭代过程中对这些合并的子区域做 bounding boxes(外切矩形),这些子区域外切矩形就是通常所说的候选框。
选择搜索的物体检测流程图:

滑窗法类似穷举进行图像子区域搜索,但是一般情况下图像中大部分子区域是没有物体的。选择搜索算法的主要观点:图像中物体可能存在的区域应该是有某些相似性或者连续性区域的。因此,选择搜索基于这一想法,采用子区域合并的方法进行提取 bounding boxes 候选边界框。
- 首先,对输入图像进行分割算法产生许多小的子区域。
- 其次,根据这些子区域之间相似性(相似性标准主要有颜色、纹理、大小等等)进行区域合并,不断的进行区域迭代合并。每次迭代过程中对这些合并的子区域做 bounding boxes(外切矩形),这些子区域外切矩形就是通常所说的候选框。
算法流程:

- step 0:生成区域集
R,具体参见论文《Efficient Graph-Based Image Segmentation》 - step 1:计算区域集
R里每个相邻区域的相似度S = {s1,s2,…} - step 2:找出相似度最高的两个区域,将其合并为新集,添加进
R - step 3:从
S中移除所有与 step 2中有关的子集 - step 4:计算新集与所有子集的相似度
- step 5:跳至 step 2,直至
S为空
相似度计算
Selective Search for Object Recognition论文考虑了颜色、纹理、尺寸和空间交叠这 4 个参数。
颜色相似度(color similarity)
将色彩空间转为 HSV,对于每一个 region 的每个通道以 bins=25 计算直方图,这样每个区域的颜色直方图有 25*3=75 个区间。 对直方图除以区域尺寸做归一化后使用下式计算相似度:

其中, 表示两个不同的 region,
表示两个不同的 region, 表示颜色直方图。
表示颜色直方图。
纹理相似度(texture similarity)
采用方差为1( )的高斯分布在
)的高斯分布在8个方向做梯度统计,然后将统计结果(尺寸与区域大小一致)以bins=10计算直方图。直方图区间数为8*3*10=240(使用RGB色彩空间)

其中, 是直方图中第
是直方图中第 个
个bin的值
尺寸相似度(size similarity)

保证合并操作的尺度较为均匀,避免一个大区域陆续“吃掉”其他小区域。
例子:
设有区域 a-b-c-d-e-f-g-h :
- 较好的合并方式是:
ab-cd-ef-gh -> abcd-efgh -> abcdefgh。 - 不好的合并方法是:
ab-c-d-e-f-g-h ->abcd-e-f-g-h ->abcdef-gh -> abcdefgh。
交叠相似度(shape compatibility measure)

例子:左图适于合并,右图不适于合并

最终的相似度

池化层
池化层可以非常有效地缩小矩阵的尺寸,从而减少最后全连接层中的参数。使用池化层,既可以加快计算速度,也有防止过拟合问题的作用。
池化层前向传播的过程也是通过移动 一个类似过滤器的结构完成的 。不过池化层过滤器中 的计算不是节点的加权和,而是采用更加简单的最大值或者平均值运算。使用最大值操作的池化层被称之为最大池化层( max pooling ),这是被使用得最多的池化层结构。使用平均值操作的池化层被称之为平均池化层( average pooling )。
卷积层和池化层中过滤器移动的方式是相似的,唯一的区别在于卷积层使用的过滤器是横跨整个深度的,而池化层使用 的过滤器只影响一个深度上的节点。所以池化层 的过滤器除了在长和宽两个维度移动 ,它还需要在深度这个维度移动。
LeNet

第一层:卷积层
这一层的输入就是原始的图像像素 , LeNet 模型接受的输入层大小为 32×32×l。第一个卷积层 filter 的尺寸为 5×5,深度为 6,不使用全 0 填充,步长为 1 。因为没有使用全 0 填充,所以这 一 层的输出 的尺寸为 32-5+1=28, 深度为 6 。这一个卷积层总共有 5×5×6+6=156 个参数,其中 6 个为偏置项参数。因为下一层的节点矩阵有 28×28=4704 个节点,每个节点和 5×5=25 个当前层节点相连,所以本 层卷积层总共有 4704×(25+1)=122304 个连接。
第二层:池化层
这一层的输入为第一层的输出, 是一个 28×28×6 的节点矩阵。本层采用的 filter 大小为 2×2,长和宽的步长均为 2,所以本层的输出矩阵大小为 14×14×6。
第三层:卷积层
本层的输入矩阵大小为 14×14×6,使用的 filter 大小为 5×5 ,深度为 16。本层不使用全 0 填充, 步长为 l。本层的输出矩阵大小为 10×10×16。按照标准的卷积层 ,本层应该有 5×5×6×16+16=2416 个参数,10×10×16×(25+1)=41600 个连接。
第四层:池化层
本层的输入矩阵大小为 10×l0×16,采用的 filter 大小为 2×2,步长为 2。本层的输出矩阵大小为 5×5×l6。
第五层:全连接层
本层的输入矩阵大小为 5×5×16,在 LeNet 模型的论文中将这一层称为卷积层,但是因为 filter 的大小就是 5×5,所以和全连接层没有区别。如果将 5×5×16 矩阵中的节点拉成一个向量,那么这一层和全连接层输入就一样了。本层的输出节点个数为 120个,总共有 5×5×16×120+120=48120 个参数。
第六层:全连接层
本层的输入节点个数为 120 个,输出节点个数为 84 个,总共参数为 120×84+84=10164个。
第七层:全连接层
本层的输入节点个数为 84 个,输出节点个数为 10 个,总共参数为 84×10+10=850 个 。
TensorFlow 的实现(LeNet.py,在 MNIST 中为 mnist_train.py):
# 配置神经网络参数
INPUT_NODE = 784
OUTPUT_NODE = 10
IMAGE_SIZE = 28
NUM_CHANNELS = 1
NUM_LABELS = 10
# 第一层卷积层的尺寸和深度
CONV1_DEEPTH = 32
CONV1_SIZE = 5
# 第二层卷积层的尺寸和深度
CONV2_DEEPTH = 64
CONV2_SIZE = 5
# 全连接层的结点个数
FC_SIZE = 512
# 次函数表示CNN的的前向传播过程。其中,train用于表示:区分训练过程还是测试过程。
def inference(input_tensor, train, regularizer):
# 第一层卷积层,和标准的LeNet模型不太一样。
# 卷积层的输入为:28*28*1 即原始的MNIST图片的像素
# 使用全0填充
# 输出为:28*28*32的矩阵
with tf.variable_scope('layer1_conv1'):
# 5*5*32
conv1_weights = tf.get_variable(
'weight',
[CONV1_SIZE, CONV1_SIZE, NUM_CHANNELS, CONV1_DEEPTH],
initializer = tf.truncated_normal_initializer(stddev=0.1)
)
conv1_biases = tf.get_variable(
'bias',
[CONV1_DEEPTH],
initializer = tf.constant_initializer(0.0)
)
# 使用边长为5,深度为32的filter,filter移动的步长为1,且使用全0填充。
conv1 = tf.nn.conv2d(
input_tensor,
conv1_weights,
strides = [1, 1, 1, 1],
padding = 'SAME'
)
relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))
with tf.name_scope('layer2_pool1'):
# 这一层的输入是上一层的输出:28*28*32
# 池化层filter为:2*2 全0填充 移动步长为2
# 输出为:14*14*32
pool1 = tf.nn.max_pool(
relu1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# 这一层的输入为:14*14*32
# 输出为:14*14*64
with tf.name_scope('layer3_conv2'):
conv2_weights = tf.get_variable(
'weight',
# 5*5*32*64
[CONV2_SIZE, CONV2_SIZE, CONV1_DEEPTH, CONV2_DEEPTH],
initializer=tf.truncated_normal_initializer(stddev=0.1))
conv2_biases = tf.get_variable(
'bias',
[CONV2_DEEPTH], # 64
initializer=tf.constant_initializer(0.0))
# 使用边长为5,深度为64的过滤器,过滤器移动的步长为1
conv2 = tf.nn.conv2d(
pool1,
conv2_weights,
strides=[1, 1, 1, 1],
padding='SAME')
relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))
# 输入为:14*14*64
# 输出为:7*7*64
with tf.name_scope('layer4_pool2'):
pool2 = tf.nn.max_pool(
relu2, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')
pool_shape = pool2.get_shape().as_list()
# pool_shape[0]:为一个 batch 中数据的大小
nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]
# 将第四层的输出转化为一个 batch 的向量
reshaped = tf.reshape(pool2, [pool_shape[0], nodes])
# 这一层的输入是拉直之后的一组向量,长度为:7*7*64=3136。输出为:512的向量
with tf.variable_scope('layer5_fc1'):
fc1_weights = tf.get_variable(
'weight',
[nodes, FC_SIZE],
initializer=tf.truncated_normal_initializer(stddev=0.1))
# 只有全连接层的权重才需要加入正则化
if regularizer != None:
tf.add_to_collection('losses', regularizer(fc1_weights))
fc1_biases = tf.get_variable(
'bias',
[FC_SIZE],
initializer=tf.constant_initializer(0.1))
fc1 = tf.nn.relu(tf.matmul(reshaped, fc1_weights) + fc1_biases)
if train:
fc1 = tf.nn.dropout(fc1, 0.5)
with tf.variable_scope('layer6_fc2'):
fc2_weights = tf.get_variable(
'weight',
[FC_SIZE, NUM_LABELS],
initializer=tf.truncated_normal_initializer(stddev=0.1))
if regularizer != None:
tf.add_to_collection('losses', regularizer(fc2_weights))
fc2_biases = tf.get_variable(
'bias',
[NUM_LABELS],
initializer=tf.constant_initializer(0.1))
logit = tf.matmul(fc1, fc2_weights) + fc2_biases
return logit
MNIST 训练过程(mnist_train.py):
import os
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 加载mnist_inference.py中定义的常量和前向传播的函数
import mnist_inference
# 配置神经网络的参数
BATCH_SIZE = 100
# 一个训练 batch 中的训练数据的数量。
# - 数字越小时,训练过程越接近随机梯度下降
# - 数字越大时,训练就越接近梯度下降
LEARNING_RATE_BASE = 0.01 # 基础学习率
LEARNING_RATE_DECAY = 0.99 # 学习率的衰减率
REGULARAZTION_RATE = 0.0001 # 正则化项中的 \lambda 系数
TRAINING_STEPS = 30000 # 训练轮数
MOVING_AVERAGE_DECAY = 0.99 # 滑动平均衰减率
# 模型保存的路径和文件名
MODEL_SAVE_PATH = "model/"
MODEL_NAME = "model.ckpt"
def train(mnist):
# 定义输入输出placeholder
# 调整输入数据placeholder的格式,输入为一个四维矩阵
x = tf.placeholder(
tf.float32,
[BATCH_SIZE, # 第一维表示一个batch中样例的个数
mnist_inference.IMAGE_SIZE, # 第二维和第三维表示图片的尺寸
mnist_inference.IMAGE_SIZE,
mnist_inference.NUM_CHANNELS], # 第四维表示图片的深度
name='x-input')
y_ = tf.placeholder(
tf.float32,
[None, mnist_inference.OUTPUT_NODE],
name='y-input')
# L2 正则化项
regularizer = tf.contrib.layers.l2_regularizer(REGULARAZTION_RATE)
# 直接使用 mnist_inference.py 中定义的前向传播过程
y = mnist_inference.inference(x, True, regularizer)
# 在使用 TensorFlow 训练神经网络时,
# 一般会将代表训练轮数的变量指定为不可训练的参数。
global_step = tf.Variable(0, trainable=False)
# 定义损失函数、学习率、滑动平均操作以及训练过程
# 创建一个滑动平均类,设置的初始滑动平均衰减率为 0.99,并设置了训练轮数
# 给定训练轮数的变量可以加快训练早期变量的更新速度。
variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
# 在所有代表神经网络参数的变量上使用滑动平均。其他辅助变量(比如 global_step)就
# 不需要。tf.trainable_variables 返回的就是图上集合 GraphKeys.TRAINABLE_VARIABLES
# 中的元索。这个集合的元索就是所有没有指定 trainable=False 的参数。
variable_averages_op = variable_averages.apply(tf.trainable_variables())
# 计算交叉熵作为刻画预训值和真实值之间差距的损失函数。这里使用了 TensorFlow 中提
# 供的 sparse_softmax_cross_entropy_with_logits 函数来计算交叉熵。当分类
# 问题只有一个正确答案时,可以使用这个函数来加速交叉熵的计算。MNIST问题的图片中
# 只包含了 0~9 中的一个数字,所以可以使用这个函数来计算交叉熵损失。
# 第一个参数是神经网络不包括 softmax 层的前向传播结果
# 第二个是训练数据的正确答案
# 因为标准答案是 1 个长度为 10 的一维数组,而该函数需要提供的是一个正确答案的数字
# 所以需要使用 tf.argmax 函数来得到正确答案对应的类别编号。
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
# 计算在当前 batch 中所有样例的交叉熵平均值。
cross_entropy_mean = tf.reduce_mean(cross_entropy)
# 总损失 = 交叉熵损 + 正正则化损失
loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
# 设置指数衰减学习率
learning_rate = tf.train.exponential_decay(
LEARNING_RATE_BASE, # 初始学习率,随着迭代的进行,更新变量时使用的学习率在这个基础上递减
global_step, # 当前迭代轮数
mnist.train.num_examples/BATCH_SIZE, # 过完所有的训练数据所需要的迭代次数
LEARNING_RATE_DECAY) # 学习率衰减速度
# 优化损失函数
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
# 在训练神经网络模型时,每过一遍数据:
# - 需要通过反向传播来更新神经网络中的参数,
# - 需要更新每一个参数的滑平均动值。
# 为了一次完成多个操作,TensorFlow 提供了tf.control_dependencies 和 tf.group 两种机制。
# 下式等价于:train_op = tf.group(train_step, variables_averages_op)
with tf.control_dependencies([train_step, variable_averages_op]):
train_op = tf.no_op(name='train')
# 初始化 Tensorflow 持久化类
saver = tf.train.Saver()
with tf.Session() as sess:
tf.global_variables_initializer().run()
# 验证和测试的过程将会有一个独立的程序来完成
# 一共训练 30000 轮
for i in range(TRAINING_STEPS):
# 每次训练所取的 batch 中的训练样本数为 100
xs, ys = mnist.train.next_batch(BATCH_SIZE)
# 将输入的训练数据格式调整为一个四维矩阵,并将这个调整后的数据传入sess.run过程
# xs 的 shape 为 (100, 784),其中 100 就是 batch_size 的大小,即 100 张图片
# 经过reshape之后,变为 (100, 28, 28, 1),100张图片,每张图片像素为 28*28,深度为 1
reshaped_xs = np.reshape(xs, ( BATCH_SIZE, # 100
mnist_inference.IMAGE_SIZE, # 28
mnist_inference.IMAGE_SIZE, # 28
mnist_inference.NUM_CHANNELS) # 1
)
# 将经过reshape之后的输入传入CNN之中,将结果保存在y_之中
_, loss_value, step = sess.run(
[train_op, loss, global_step],
feed_dict={x: reshaped_xs, y_: ys})
# 每1000轮保存一次模型。
if i % 1000 == 0:
# 输出当前的训练情况。这里只输出了模型在当前训练batch上的损失函数大小。通过损失函数的大小可以大概了解训练的情况。
# 在验证数据集上的正确率信息会有一个单独的程序来生成。
print("After %d training step(s), loss on training batch is %f." % (step, loss_value))
# 保存当前的模型。这里给出了global_step参数,这样可以让每个被保存模型的文件名末尾加上训练的轮数,比如“model.ckpt-1000”表示训练1000轮后得到的模型
saver.save(sess, os.path.join(MODEL_SAVE_PATH, MODEL_NAME), global_step=global_step)
def main(argv=None):
mnist = input_data.read_data_sets("dataset/", False, one_hot=True)
train(mnist)
if __name__ == '__main__':
tf.app.run()
接下来,就是验证(mnist_eval.py):
import time
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 加载mnist_inference.py 和 mnist_train.py中定义的常量和函数
import mnist_inference
import mnist_train
# 每10秒加载一次最新的模型, 并在测试数据上测试最新模型的正确率
EVAL_INTERVAL_SECS = 10
def evaluate(mnist):
with tf.Graph().as_default() as g:
# 定义输入输出的格式
x = tf.placeholder(
tf.float32,
[mnist.validation.num_examples, # 第一维表示样例的个数
mnist_inference.IMAGE_SIZE, # 第二维和第三维表示图片的尺寸
mnist_inference.IMAGE_SIZE,
mnist_inference.NUM_CHANNELS],
name='x-input')
y_ = tf.placeholder(
tf.float32,
[None, mnist_inference.OUTPUT_NODE],
name='y-input')
validate_feed = {
x: np.reshape(mnist.validation.images,
(mnist.validation.num_examples,
mnist_inference.IMAGE_SIZE,
mnist_inference.IMAGE_SIZE,
mnist_inference.NUM_CHANNELS)),
y_: mnist.validation.labels
}
# 直接通过调用封装好的函数来计算前向传播的结果。
# 因为测试时不关注正则损失的值,所以这里用于计算正则化损失的函数被设置为None。
y = mnist_inference.inference(x, False, None)
# 使用前向传播的结果计算正确率。
# 如果需要对未知的样例进行分类,那么使用tf.argmax(y,1)就可以得到输入样例的预测类别了。
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# 通过变量重命名的方式来加载模型,这样在前向传播的过程中就不需要调用求滑动平均的函数来获取平局值了。
# 这样就可以完全共用mnist_inference.py中定义的前向传播过程
variable_averages = tf.train.ExponentialMovingAverage(mnist_train.MOVING_AVERAGE_DECAY)
variable_to_restore = variable_averages.variables_to_restore()
saver = tf.train.Saver(variable_to_restore)
#每隔EVAL_INTERVAL_SECS秒调用一次计算正确率的过程以检测训练过程中正确率的变化
while True:
with tf.Session() as sess:
# tf.train.get_checkpoint_state函数会通过checkpoint文件自动找到目录中最新模型的文件名
ckpt = tf.train.get_checkpoint_state(mnist_train.MODEL_SAVE_PATH)
if ckpt and ckpt.model_checkpoint_path:
# 加载模型
saver.restore(sess, ckpt.model_checkpoint_path)
# 通过文件名得到模型保存时迭代的轮数
global_step = ckpt.model_checkpoint_path.split('/')[-1].split('-')[-1]
accuracy_score = sess.run(accuracy, feed_dict = validate_feed)
print("After %s training step(s), validation accuracy = %f" % (global_step, accuracy_score))
else:
print("No checkpoint file found")
return
time.sleep(EVAL_INTERVAL_SECS)
def main(argv=None):
mnist = input_data.read_data_sets("dataset/", one_hot=True)
evaluate(mnist)
if __name__ == '__main__':
tf.app.run()
以下是自己手写图片的识别:
import time
import numpy as np
import tensorflow as tf
from PIL import Image
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
# 加载mnist_inference.py 和 mnist_train.py中定义的常量和函数
import mnist_inference
import mnist_train
def evaluate(image_array):
with tf.Graph().as_default() as g:
# 定义输入输出的格式
x = tf.placeholder(
tf.float32,
[1, # 第一维表示样例的个数
mnist_inference.IMAGE_SIZE, # 第二维和第三维表示图片的尺寸
mnist_inference.IMAGE_SIZE,
mnist_inference.NUM_CHANNELS], # 第四维表示图片的深度
name='x-input')
y = mnist_inference.inference(x, False, None)
prediction_value = tf.argmax(y, 1)
# 通过变量重命名的方式来加载模型,这样在前向传播的过程中就不需要调用求滑动平均的函数来获取平局值了。
# 这样就可以完全共用mnist_inference.py中定义的前向传播过程
variable_averages = tf.train.ExponentialMovingAverage(mnist_train.MOVING_AVERAGE_DECAY)
variable_to_restore = variable_averages.variables_to_restore()
saver = tf.train.Saver(variable_to_restore)
with tf.Session() as sess:
# tf.train.get_checkpoint_state函数会通过checkpoint文件自动找到目录中最新模型的文件名
ckpt = tf.train.get_checkpoint_state(mnist_train.MODEL_SAVE_PATH)
if ckpt and ckpt.model_checkpoint_path:
# 加载模型
saver.restore(sess, ckpt.model_checkpoint_path)
# 通过文件名得到模型保存时迭代的轮数
prediction_value = sess.run(prediction_value,
feed_dict={x: np.reshape(image_array, (1, mnist_inference.IMAGE_SIZE, mnist_inference.IMAGE_SIZE, mnist_inference.NUM_CHANNELS))})
return prediction_value
else:
print("No checkpoint file found")
return
# def pre_pic(picName):
# # 先打开传入的原始图片
# img = Image.open(picName)
# # 使用消除锯齿的方法resize图片
# reIm = img.resize((28,28),Image.ANTIALIAS)
# # 变成灰度图,转换成矩阵
# im_arr = np.array(reIm.convert("L"))
# threshold = 50#对图像进行二值化处理,设置合理的阈值,可以过滤掉噪声,让他只有纯白色的点和纯黑色点
# for i in range(28):
# for j in range(28):
# im_arr[i][j] = 255-im_arr[i][j]
# if (im_arr[i][j]<threshold):
# im_arr[i][j] = 0
# else:
# im_arr[i][j] = 255
# # 将图像矩阵拉成1行784列,并将值变成浮点型(像素要求的仕0-1的浮点型输入)
# nm_arr = im_arr.reshape([1,784])
# nm_arr = nm_arr.astype(np.float32)
# img_ready = np.multiply(nm_arr,1.0/255.0)
# return img_ready
# 图片预处理函数
def process_image():
file_name='pic/2.png' # 导入自己的图片地址
image = Image.open(file_name).convert('L')
image_array = [(255-x)*1.0/255.0 for x in list(image.getdata())]
return image_array
def main(argv=None):
image_array = process_image()
# 将处理后的结果输入到预测函数最后返回预测结果
prediction_value = evaluate(image_array)
print("The prediction number is : ", prediction_value)
if __name__ == '__main__':
tf.app.run()
# 从mnist中读取数字
# mnist = input_data.read_data_sets("dataset/", False, one_hot=True)
# tf.reset_default_graph()
# im = mnist.test.images[1].reshape((28,28))
# img = Image.fromarray(im*255)
# img = img.convert('RGB')
# img.save(r'pic\2.jpg')
# plt.imshow(im, cmap="gray")
# plt.show()
如何设计卷积神经网络的架构呢?以下正则表达式公式总结了一些经典的用于图片分类问题的卷积神经网络架构 :
输入层 --> (卷积层+ --> 池化层?)+ --> 全连接层+
在以上公式中:
卷积层+表示一层或者多层卷积层,大部分卷积神经网络中一般最多连续使用三层卷积层。池化层?表示没有或者一层池化层。池化层虽然可以起到减少参数防止过拟合问题,但是在部分论文中也发现可以直接通过调整卷积层步长来完成。 所以有些卷积神经网络中没有地化层。在多轮卷积层和池化层之后,卷积神经网络在输出之前一般会经过1~2个全连接层。
比如 LeNet-5 模型就可以表示为以下结构。
输入层 --> 卷积层 --> 池化层 --> 卷积层 --> 池化层 --> 全连接层 --> 全连接层 --> 输出层
在输入和输出层之间的神经网络叫做隐藏层, 一般一个神经网络的隐藏层越多,这个神经网络越“深”。而所谓深度学习中的这个“深度”和神经网络的层数也是密切相关的。
RCNN
整体过程:
- 输入一张多目标图像,采用 selective search 算法提取约
2000个建议框 - 先在每个建议框周围加上
16个像素值为建议框像素平均值的边框,再直接变形为227×227的大小 - 先将所有建议框像素减去该建议框像素平均值后【预处理操作】,再依次将每个
227×227的建议框输入 AlexNet CNN 网络获取4096维的特征【比以前的人工经验特征低两个数量级】,2000个建议框的CNN特征组合成2000×4096维矩阵 - 将
2000×4096维特征与20个 SVM 组成的权值矩阵4096×20相乘【20种分类,SVM 是二分类器,则有20个 SVM】,获得2000×20维矩阵表示每个建议框是某个物体类别的得分 - 分别对上述
2000×20维矩阵中每一列即每一类进行非极大值抑制剔除重叠建议框,得到该列即该类中得分最高的一些建议框 - 分别用
20个回归器对上述20个类别中剩余的建议框进行回归操作,最终得到每个类别的修正后的得分最高的 bounding box
1. 算法的整体思路
通过利用 recongnition using regions 操作来解决 CNN 的定位问题,此方法在目标检测和语义分割中都取得了成功。测试阶段,此方法对每一个输入的图片产生近 2000 个不分种类的 region proposals,使用 CNN 从每个 region proposals 中提取一个固定长度的特征向量,然后对每个 region proposal 提取的特征向量使用特定种类的线性SVM进行分类(CNN + SVM for classification)。
RCNN 采用的方法是:首先输入一张图片,先定位出 2000 个物体候选框,然后采用 CNN 提取每个候选框中图片的特征向量,特征向量的维度为 4096 维,接着采用 SVM 算法对各个候选框中的物体进行分类识别。
RCNN 算法主要分为四个步骤:
- 找出候选框(一张图像生成
1K~2K个候选区域 ) - 利用 CNN 提取特征向量(对每个候选区域,使用深度网络提取特征 )
- 利用 SVM 进行特征向量分类( 特征送入每一类的 SVM 分类器,判别是否属于该类)
- 使用回归器精细修正候选框位置

2. 候选框的搜索
当输入一张图片时,搜索出所有可能是物体的区域,这个采用的方法是传统文献的算法:《Selective Search for Object Recognition》,通过这个算法可以搜索出 2000 个候选框(搜出的候选框是矩形的,而且是大小各不相同)。然而,CNN 对输入图片的大小的要求是固定的,如果把搜索到的矩形选框不做处理,就扔进 CNN 中,肯定不行。
因此,对于每个输入的候选框都需要缩放到固定的大小。为了简单起见,假设下一阶段 CNN 所需要的输入图片大小是个正方形图片:227×227。由于经过 selective search 得到的是矩形框,可以采用两种不同的处理方法:
1. 各向异性缩放
即不管图片的长宽比例,也不管其是否扭曲,直接缩放成 CNN 输入的大小 227×227(如图 (D) 所示)。
2. 各向同性缩放
因为图片扭曲后,可能会对后续 CNN 的训练精度有影响。各向同性缩放有两种方案:
- 直接在原始图片中,把 bounding box 的边界扩展延伸成正方形,然后再进行裁剪;如果已经延伸到了原始图片的外边界,那么就用 bounding box 中的颜色均值填充(如图
(B)所示)。 - 先把 bounding box 图片裁剪出来,然后用固定的背景颜色填充成正方形图片(背景颜色也采用 bounding box 的像素颜色均值,如图
(C)所示)。

得到指定大小的图片后,后面还要继续用这 2000 个候选框图片继续训练 CNN、SVM。在一张图中,人工标注时就只标注了正确的 bounding box,搜索出来的 2000 个矩形框不可能会出现一个与人工标注完全匹配的候选框。
因此,需要用 IoU 为 2000 个 bounding box 打标签,以便下一步 CNN 训练使用。在 CNN 阶段,如果用 selective search 挑选出来的候选框与物体的人工标注矩形框的重叠 IoU 大于 0.5,就把这个候选框标注成物体类别,否则就把它当做背景类别。
非极大值抑制的具体操作
在测试过程完成到第 4 步之后,获得 2000×20 维矩阵表示每个建议框是某个物体类别的得分情况,此时会遇到下图所示情况,同一个车辆目标会被多个建议框包围,这时需要非极大值抑制操作去除得分较低的候选框以减少重叠框。

步骤:
- 对
2000×20维矩阵中每列按从大到小进行排序 - 从每列最大的得分建议框开始,分别与该列后面的得分建议框进行
IoU计算,若IoU > 阈值,则剔除得分较小的建议框,否则认为图像中存在多个同一类物体 - 从每列次大的得分建议框开始,重复步骤
2 - 重复步骤
3,直到遍历完该列所有建议框 - 遍历完
2000×20维矩阵所有列,即所有物体种类都做一遍非极大值抑制 - 最后剔除各个类别中剩余建议框得分少于该类别阈值的建议框
3. CNN特征提取
1. 网络结构设计
网络结构有两个可选方案:
- 经典的 Alexnet
- VGG16
经过测试,Alexnet 精度为 58.5%,VGG16 精度为 66%。 VGG 模型的特点是:选择比较小的卷积核、选择较小的跨步,这个网络的精度高,不过计算量是 Alexnet 的 7 倍。为简单起见,直接选用 Alexnet。Alexnet 特征提取部分包含了 5 个卷积层、3 个全连接层,在 Alexnet 中 p5 层神经元个数为 9216,f6、f7 的神经元个数都是 4096,通过这个网络训练完毕后,最后提取特征每个输入候选框图片都能得到一个 4096 维的特征向量。
2. 有监督预训练
参数初始化部分:物体检测的一个难点在于,物体标签训练数据少,如果直接采用随机初始化 CNN 参数的方法,那么目前的训练数据量是远远不够的。
这种情况下,最好的是采用某些方法,把参数初始化了,然后再进行有监督的参数微调。RCNN 采用有监督的预训练,所以在设计网络结构时,直接用 Alexnet 的网络(连参数也是直接采用它的参数,作为初始的参数值,然后再 fine-tuning 训练)。网络优化求解:采用随机梯度下降法,学习速率大小为 0.001。
3. fine-tuning 训练
采用 selective search 搜索出来的候选框,处理到指定的大小,继续对上面预训练的 CNN 模型进行 fine-tuning 训练。
假设要检测的物体类别有 N 类,那么就需要把上面预训练阶段的 CNN 模型的最后一层给替换掉,替换成 N+1 个输出的神经元(加 1,表示还有一个背景),然后这一层直接采用参数随机初始化的方法,其它网络层的参数不变。接着进行 SGD 训练。开始的时候,SGD 学习率选择 0.001,在每次训练的时候,batch size 大小选择 128(其中,32 个为正样本、96 个为负样本)。
疑问
1. 既然 CNN 都是用于提取特征,那么直接用 Alexnet 做特征提取,省去 fine-tuning 阶段可以吗?
可以。可以不需重新训练 CNN,直接采用 Alexnet 模型,提取出 p5 或者 f6、f7 的特征作为特征向量,然后进行训练 SVM(只不过这样精度会比较低)。
2. 没有 fine-tuning 的时候,要选择哪一层的特征作为 CNN 提取到的特征呢?由于可以选择 p5、f6、f7,这三层的神经元个数分别是 9216、4096、4096。从 p5 到 p6 这层的参数个数是:4096*9216,从 f6 到 f7 的参数是4096*4096。那么具体是选择 p5、f6 还是 f7 呢?
RCNN 论文证明了一个理论:如果不进行 fine-tuning,即直接把 Alexnet 模型当做万金油使用,类似于 HOG、SIFT 一样做特征提取,不针对特定的任务,然后把提取的特征用于分类,结果发现 p5 的精度竟然跟 f6、f7 差不多,而且 f6 提取到的特征还比 f7 的精度略高;如果进行了 fine-tuning,那么 f7、f6 提取到的特征就会让训练的 SVM 分类器的精度飙涨。
据此,如果不针对特定任务进行 fine-tuning,而是把 CNN 当做特征提取器的话,卷积层所学到的特征其实就是基础的共享特征提取层,就类似于 SIFT 算法一样,可以用于提取各种图片的特征,而 f6、f7 所学习到的特征是用于针对特定任务的特征。打个比方:对于人脸性别识别来说,一个 CNN 模型前面的卷积层所学习到的特征就类似于学习人脸共性特征,然后全连接层所学习的特征就是针对性别分类的特征。
3. CNN 在进行训练的时候,本来就是对 bounding box 的物体进行识别分类训练,是一个端到端的任务。在训练的最后一层 softmax 就是分类层,那么为什么要先用 CNN 做特征提取(提取 fc7层数据),然后再把提取的特征用于训练 SVM 分类器?
这是因为 SVM 训练和 CNN 训练过程的正负样本定义方式各有不同,导致最后采用 CNN softmax 输出比采用 SVM 精度还低。
CNN 在训练的时候,对训练数据做了比较宽松的标注(比如一个 bounding box 可能只包含物体的一部分),那么把它也标注为正样本,用于训练 CNN;采用这个方法的主要原因在于 CNN 容易过拟合,所以需要大量的训练数据。在 CNN 训练阶段,是对 bounding box 的位置限制条件限制的比较松(IoU 只要大于 0.5 都被标注为正样本);
然而 SVM 训练的时候,因为 SVM 适用于少样本训练,所以对于训练样本数据的 IoU 要求比较严格,只有当bounding box 把整个物体都包含进去了,才把它标注为物体类别,然后训练 SVM。
4. 为什么需要回归器?
目标检测不仅是要对目标进行识别,还要完成定位任务,所以最终获得的bounding-box也决定了目标检测的精度(定位精度可以用算法得出的物体检测框与实际标注的物体边界框的IoU值来近似表示)。
如下图所示,绿色框为实际标准的卡宴车辆框,即Ground Truth;黄色框为selective search算法得出的建议框,即Region Proposal。即使黄色框中物体被分类器识别为卡宴车辆,但是由于绿色框和黄色框IoU值并不大,所以最后的目标检测精度并不高。采用回归器是为了对建议框进行校正,使得校正后的Region Proposal与selective search更接近, 以提高最终的检测精度。

如何设计回归器(Bounding-box regression)?
如下图所示,黄色框口P表示建议框Region Proposal,绿色窗口G表示实际框Ground Truth,红色窗口表示Region Proposal进行回归后的预测窗口。现在的目标是:找到P的线性变换【当Region Proposal与Ground Truth的IoU > 0.6时,可以认为是线性变换】,使得与G越相近,这就相当于一个可以用最小二乘法解决的线性回归问题。

P窗口的数学表达式: ,其中表示第
,其中表示第i个窗口的中心点坐标, 分别为第
分别为第i个窗口的宽和高
G窗口的数学表达式为: 。
。
定义四种变换函数 和
和 (即,通过平移对
(即,通过平移对x和y进行变化,通过缩放对w和h进行变化):

每一个函数 【
【 表示
表示 中的一个】都是一个AlexNet CNN网络的
中的一个】都是一个AlexNet CNN网络的 层特征(用
层特征(用 表示)的线性函数。所以有
表示)的线性函数。所以有 ,其中,
,其中, 为可学习模型参数(learnable
为可学习模型参数(learnable
model parameters)的向量,它就是所需要学习的回归参数。
损失函数(使用岭回归)为:

损失函数中加入正则项是为了避免归回参数过大。其中,回归目标( )由训练输入对按下式计算得来:
)由训练输入对按下式计算得来:

回归的整体过程为:
- 构造样本对。为了提高每类样本框回归的有效性,对每类样本都仅仅采集与Ground Truth相交
IoU最大的Region Proposal,并且IoU > 0.6的Region Proposal作为样本对,一共产生20对样本对【20个类别】 - 每种类型的回归器进行单独训练,输入该类型样本对
N个以及其所对应的AlexNet CNN网络 层特征
层特征 - 利用
(6)-(9)式和输入样本对进行计算 - 根据损失函数
(5)进行回归,得到使损失函数最小的参数
4. SVM训练
这是一个二分类问题,我么假设要检测车辆。只有当bounding box把整量车都包含在内,那才叫正样本;如果bounding box 没有包含到车辆,那么就可以把它当做负样本。
但问题是当检测窗口只有部分包含物体,那该怎么定义正负样本呢?通过训练发现,如果选择IoU阈值为0.3效果最好,即当重叠度小于0.3的时候,就把它标注为负样本。一旦CNN f7层特征被提取出来,那么将为每个物体累训练一个SVM分类器。当用CNN提取2000个候选框,可以得到2000×4096的特征向量矩阵,然后只需要把这样的一个矩阵与SVM权值矩阵4096×N点乘(N为分类类别数目,因为训练的N个SVM,每个SVM包含了4096个W),就可以得到结果。
图片分类标注好的训练数据非常多,但是物体检测的标注数据却很少,如何用少量的标注数据,训练高质量的模型,这就是RCNN最大的特点。其采用了迁移学习的思想:先利用ILSVRC2012这个训练数据库(一个图片分类训练数据库,其拥有大量的标注数据,共包含了1000种类别物体),进行网络的图片分类训练。因此,预训练阶段CNN模型的输出是1000个神经元,或者也可以直接采用Alexnet训练好的模型参数。
扩展阅读:
Faster RCNN
经过 R-CNN 和 Fast RCNN 的积淀,Ross B. Girshick 在 2016 年提出了新的 Faster RCNN,在结构上,Faster RCNN 已经将特征抽(feature extraction),proposal 提取,bounding box regression(rect refine),classification 都整合在了一个网络中,使得综合性能有较大提高,在检测速度方面尤为明显。

依作者看来,如上图,Faster RCNN 其实可以分为 4 个主要内容:
- Conv layers。作为一种 CNN 网络目标检测方法,Faster RCNN 首先使用一组基础的
conv + relu + pooling层提取 image 的 feature maps。该 feature maps 被共享用于后续 RPN 层和全连接层。 - Region Proposal Networks。RPN 网络用于生成 region proposals。该层通过 softmax 判断 anchors 属于 foreground 或者 background,再利用 bounding box regression 修正 anchors 获得精确的 proposals。
- Roi Pooling。该层收集输入的 feature maps 和 proposals,综合这些信息后提取 proposal feature maps,送入后续全连接层判定目标类别。
- Classification。利用 proposal feature maps 计算 proposal 的类别,同时再次 bounding box regression 获得检测框最终的精确位置。
所以本文以上述 4 个内容作为切入点介绍 Faster R-CNN 网络。下图展示了Python 版本中的 VGG16 模型中的 faster_rcnn_test.py 的网络结构,可以清晰的看到该网络对于一副任意大小 PxQ 的图像:
- 首先缩放至固定大小
MxN,然后将MxN图像送入网络 - 而 Conv layers 中包含了
13个conv层 +13个relu层 +4个pooling层 - RPN 网络首先经过
3x3卷积,再分别生成 foreground anchors 与 bounding box regression 偏移量,然后计算出 proposals - 而 Roi Pooling 层则利用 proposals 从 feature maps 中提取 proposal feature 送入后续全连接和 softmax 网络作 classification(即分类 proposal 到底是什么 object)

1. Conv layers
Conv layers 包含了 conv,pooling,relu 三种层。以 Python版本中的 VGG16 模型中的 faster_rcnn_test.py 的网络结构为例,如上图。Conv layers 部分共有 13 个 conv 层,13 个 relu 层,4 个 pooling 层。在 Conv layers 中:
- 所有的
conv层为:kernel_size = 3padding = 1stride = 1
- 所有的
pooling层为:kernel_size = 2padding = 0stride = 2
在 Faster RCNN Conv layers 中对所有的卷积都做了扩边处理( padding=1,即填充一圈 0),导致原图变为 (M+2)x(N+2) 大小,再做 3x3 卷积后输出 MxN。正是这种设置,导致 Conv layers 中的 conv 层不改变输入和输出矩阵大小。如下图所示:

类似的是,Conv layers 中的 pooling 层 kernel_size=2,stride=2。这样,·每个经过 pooling 层的 MxN 矩阵,都会变为 (M/2)x(N/2) 大小。综上所述,在整个 Conv layers 中,conv 和 relu 层不改变输入输出大小,只有 pooling 层使输出长宽都变为输入的 1/2。
那么,一个 MxN 大小的矩阵经过 Conv layers 固定变为 (M/16)x(N/16)。这样 Conv layers 生成的 feature map 中都可以和原图对应起来。
2. Region Proposal Networks(RPN)
经典的检测方法生成检测框都非常耗时,如 OpenCV adaboost 使用滑动窗口 + 图像金字塔生成检测框;或如 R-CNN 使用 SS(Selective Search)方法生成检测框。而 Faster RCNN 则抛弃了传统的滑动窗口和 SS 方法,直接使用 RPN 生成检测框,这也是 Faster R-CNN 的巨大优势,能极大提升检测框的生成速度。

上图展示了 RPN 网络的具体结构。可以看到 RPN 网络实际分为两条线:
- 上面一条通过 softmax 分类 anchors 获得 foreground 和 background(检测目标是 foreground)
- 下面一条用于计算对于 anchors 的 bounding box regression 偏移量,以获得精确的 proposal。
最后的 Proposal 层则负责综合 foreground anchors 和 bounding box regression 偏移量获取 proposals,同时剔除太小和超出边界的 proposals。其实整个网络到了 Proposal Layer 这里,就完成了相当于目标定位的功能。
2.1 多通道图像卷积基础知识介绍
- 对于单通道图像+单卷积核做卷积,比较简单。
- 对于多通道图像+多卷积核做卷积,计算方式如下:

如上图,输入有 3 个通道,同时有 2 个卷积核。对于每个卷积核,先在输入 3 个通道分别作卷积,再将 3 个通道结果加起来得到卷积输出。所以对于某个卷积层,无论输入图像有多少个通道,输出图像通道数总是等于卷积核数量。
对多通道图像做 1x1 卷积,其实就是将输入图像于每个通道乘以卷积系数后加在一起,即相当于把原图像中本来各个独立的通道“联通”在了一起。
2.2 anchors
与 RPN 网络密切相关的是 anchors。anchors,实际上就是一组由rpn/generate_anchors.py 生成的矩形。直接运行作者 demo 中的 generate_anchors.py 可以得到以下输出:

其中每行的 4 个值  表矩形左上和右下角点坐标。
表矩形左上和右下角点坐标。9 个矩形共有 3 种形状,长宽比为大约为:  三种,如下图。实际上通过 anchors 就引入了检测中常用到的多尺度方法。
三种,如下图。实际上通过 anchors 就引入了检测中常用到的多尺度方法。

注:关于上面的 anchors size,其实是根据检测图像设置的。在 Python demo 中,会把任意大小的输入图像 reshape 成 800x600(即之前图中的M=800,N=600)。再回头来看 anchors 的大小,anchors 中长宽 1:2 中最大为 352x704,长宽 2:1 中最大 736x384,基本是 cover 了 800x600 的各个尺度和形状。
那么这 9 个 anchors 是做什么的呢?借用 Faster RCNN 论文中的原图,如图7,遍历 Conv layers 计算获得的 feature maps,为每一个点都配备这 9 种 anchors 作为初始的检测框。这样做获得检测框很不准确,不用担心,后面还有 2 次 bounding box regression 可以修正检测框位置。

解释一下上面这张图的数字:
- 在原文中使用的是 ZF model 中,其 Conv Layers 中最后的
conv5层num_output=256,对应生成256张特征图,所以相当于 feature map 每个点都是256-dimensions - 在
conv5之后,做了rpn_conv/3x3卷积且num_output=256,相当于每个点又融合了周围3x3的空间信息(猜测这样做也许更鲁棒?反正我没测试),同时256-d不变 - 假设在
conv5feature map 中每个点上有k个 anchor(默认k=9),而每个 anchor 要分 foreground 和 background,所以每个点由256dfeature 转化为cls=2k scores;而每个 anchor 都有(x, y, w, h)对应4个偏移量,所以reg=4k coordinates - 补充一点,全部 anchors 拿去训练太多了,训练程序会在合适的 anchors 中随机选取
128个 positive anchors +128个negative anchors 进行训练(什么是合适的 anchors 下文解释)
注意,在本文使用的 VGG conv5 num_output=512,所以是 512d,其他类似。
其实 RPN 最终就是在原图尺度上,设置了密密麻麻的候选 anchor。然后用 CNN 去判断哪些 anchor是里面有目标的 foreground anchor,哪些是没目标的 background。所以,仅仅是个二分类而已。
那么 anchor 一共有多少个?原图 800x600,VGG 下采样 16 倍,feature map 每个点设置 9 个 anchor,所以:

其中 ceil() 表示向上取整,是因为 VGG 输出的 feature map size= 50*38。

2.3 softmax 判定 foreground 与 background
一副 MxN 大小的矩阵送入 Faster RCNN 网络后,到 RPN 网络变为 (M/16)x(N/16),不妨设 W=M/16,H=N/16。在进入 reshape 与 softmax 之前,先做了 1x1 卷积,如下图:

该 1x1 卷积的 caffe prototxt 定义如下:
layer {
name: "rpn_cls_score"
type: "Convolution"
bottom: "rpn/output"
top: "rpn_cls_score"
convolution_param {
num_output: 18 # 2(bg/fg) * 9(anchors)
kernel_size: 1 pad: 0 stride: 1
}
}
可以看到其 num_output=18,也就是经过该卷积的输出图像为 WxHx18 大小。这也就刚好对应了 feature maps 每一个点都有 9 个 anchors,同时每个 anchors 又有可能是 foreground 和 background,所有这些信息都保存 WxHx(9*2) 大小的矩阵。
为何这样做?后面接 softmax 分类获得 foreground anchors,也就相当于初步提取了检测目标候选区域 box(一般认为目标在 foreground anchors 中)。
那么为何要在 softmax 前后都接一个 reshape layer?其实只是为了便于 softmax 分类,至于具体原因这就要从 caffe 的实现形式说起了。在 caffe 基本数据结构 blob 中以如下形式保存数据:
blob=[batch_size, channel,height,width]
对应至上面的保存 bg/fg anchors的矩阵,其在 caffe blob 中的存储形式为 [1, 2x9, H, W]。而在 softmax 分类时需要进行 fg/bg 二分类,所以 reshape layer 会将其变为 [1, 2, 9xH, W] 大小,即单独“腾空”出来一个维度以便 softmax 分类,之后再 reshape 回复原状。贴一段 caffe softmax_loss_layer.cpp 的 reshape 函数的解释,非常精辟:
"Number of labels must match number of predictions; "
"e.g., if softmax axis == 1 and prediction shape is (N, C, H, W), "
"label count (number of labels) must be N*H*W, "
"with integer values in {0, 1, ..., C-1}.";
综上所述,RPN 网络中利用 anchors 和 softmax 初步提取出 foreground anchors 作为候选区域。
2.4 bounding box regression 原理
目标检测中 region proposal 的作用?
1. 理由一
以 Faster RCNN 举例。在 Faster RCNN 里面,anchor(或者说 RPN 网络)的作用是代替以往 RCNN 使用的 selective search 的方法寻找图片里面可能存在物体的区域。当一张图片输入 Resnet 或者 VGG,在最后一层的 feature map 上面,寻找可能出现物体的位置,这时候分别以这张 feature map 的每一个点为中心,在原图上画出 9 个尺寸不一的 anchor。然后计算 anchor 与GT(ground truth) box 的 IoU(重叠率),满足一定 IoU 条件的 anchor,便认为是这个 anchor 包含了某个物体。
目标检测的思想是,首先在图片中寻找“可能存在物体的位置(regions)”,然后再判断“这个位置里面的物体是什么东西”,所以region proposal就参与了判断物体可能存在位置的过程。
region proposal 是让模型学会去看哪里有物体,GT box 就是给它进行参考,告诉它是不是看错了,该往哪些地方看才对。
2. 理由二
首先明确一个定义,当前主流的 Object Detection 框架分为 one-stage 和 two-stage,而 two-stage 多出来的这个 stage 就是 Regional Proposal 过程。
Regional Proposal的输出到底是什么?以 Faster R-CNN 为代表的 two-stage 目标检测方法为例:

可以看到,图中有两个 Classification loss 和两个 Bounding-box regression loss,有什么区别呢?
- Input Image 经过 CNN 特征提取,首先来到 Region Proposal 网络。由 Region Proposal Network 输出的Classification,这并不是判定物体在 COCO 数据集上对应的
80类中哪一类,而是输出一个二进制值p,可以理解为,人工设定一个
threshold=0.5。 - RPN 网络做的事情就是,如果一个 Region 的
,则认为这个 Region 中可能是
80个类别中的某一类,具体是哪一类现在还不清楚。到此为止,Network 只需要把这些可能含有物体的区域选取出来就可以了,这些被选取出来的 Region 又叫做 ROI (Region of Interests),即感兴趣的区域。当然了,RPN 同时也会在 feature map 上框定这些 ROI 感兴趣区域的大致位置,即输出 Bounding-box。
所以,RPN 网络做的事情就是,把一张图片中不感兴趣的区域—花花草草、大马路、天空之类的区域忽视掉,只留下一些可能感兴趣的区域—车辆、行人、水杯、闹钟等等,然后之后只需要关注这些感兴趣的区域,进一步确定它到底是车辆、还是行人、还是水杯(分类问题)等。到此为止,RPN 网络的工作就完成了,即我们现在得到的有:在输入 RPN 网络的 feature map 上,所有可能包含 80 类物体的 Region 区域的信息,其他 Region(非常多)可以直接不考虑了(不用输入后续网络)。
接下来的工作就很简单了,假设输入 RPN 网络的 feature map 大小为 ,那么提取的 ROI 的尺寸一定小于
,因为原始图像某一块的物体在 feature map 上也以同样的比例存在。只需要把这些 Region 从 feature map 上抠出来,由于每个 Region 的尺寸可能不一样,因为原始图像上物体大小不一样,所以我们需要将这些抠出来的 Region 想办法 resize 到相同的尺寸,这一步方法很多(Pooling 或者 Interpolation,一般采用 Pooling,因为反向传播时求导方便)。
假设这些抠出来的 ROI Region 被 resize 到了 或者
,那接下来将这些 Region 输入普通的分类网络,即第一张 Faster R-CNN 的结构图中最上面的部分,即可得到整个网络最终的输出 classification,这里的 class(车、人、狗 ……)才真正对应了 COCO 数据集
80 类中的具体类别。
同时,由于之前 RPN 确定的 box\region 坐标比较粗略,即大概框出了感兴趣的区域,所以这里再来一次精确的微调,根据每个 box 中的具体内容微微调整一下这个 box的坐标,即输出第一张图中右上方的 Bounding-box regression。
总结
Region Proposal有什么作用?
- COCO 数据集上总共只有
80类物体,如果不进行 Region Proposal,即网络最后的 classification 是对所有 anchor 框定的 Region 进行识别分类,会严重拖累网络的分类性能,难以收敛。原因在于,存在过多的不包含任何有用的类别(80类之外的,例如各种各样的天空、草地、水泥墙、玻璃反射等等)的 Region 输入分类网络,而这些无用的 Region 占了所有 Region 的很大比例。换句话说,这些 Region 数量庞大,却并不能为 softmax 分类器带来有用的性能提升(因为无论怎么预测,其类别都是背景,对于主体的80类没有贡献)。 - 大量无用的 Region 都需要单独进入分类网络,而分类网络由几层卷积层和最后一层全连接层组成,参数众多,十分耗费计算时间,Faster R-CNN 本来就不能做到实时,这下更慢了。
SPP Net
出自 2015 年发表在 IEEE 上的论文—《Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition》
在此之前,所有的神经网络都是需要输入固定尺寸的图片,比如 224x224(AlexNet)、32x32(LeNet)、96x96 等。这样对于希望检测各种大小的图片的时候,需要经过 crop,或者 war p等一系列操作,这都在一定程度上导致图片信息的丢失和变形,限制了识别精确度。
RCNN 的弊端
RCNN 使用 CNN 作为特征提取器,首次使得目标检测跨入深度学习的阶段。但是 RCNN 对于每一个区域候选都需要首先将图片放缩到固定的尺寸(224x224),然后为每个区域候选提取 CNN 特征。容易看出这里面存在的一些性能瓶颈:
- 速度瓶颈:重复为每个 region proposal 提取特征是极其费时的,Selective Search 对于每幅图片产生
2K左右个 region proposal,也就是意味着一幅图片需要经过2K次的完整的 CNN 计算得到最终的结果。 - 性能瓶颈:对于所有的 region proposal 防缩到固定的尺寸会导致我们不期望看到的几何形变,而且由于速度瓶颈的存在,不可能采用多尺度或者是大量的数据增强去训练模型。
在 RCNN 中 CNN 阶段的流程大致如下(红色框是 selective search 输出的可能包含物体的候选框(ROI)):

上面这个图可以看出SPP Net 和 RCNN 的区别,首先是输入不需要放缩到指定大小。其次是增加了一个空间金字塔池化层,还有最重要的一点是每幅图片只需要提取一次特征。
为什么要固定输入图片的大小?
卷积层的参数和输入大小无关,它仅仅是一个卷积核在图像上滑动,不管输入图像多大都没关系,只是对不同大小的图片卷积出不同大小的特征图,但是全连接层的参数就和输入图像大小有关,因为它要把输入的所有像素点连接起来,需要指定输入层神经元个数和输出层神经元个数,所以需要规定输入的 feature 的大小。因此,固定长度的约束仅限于全连接层(作为全连接层,如果输入的 x 维数不等,那么参数 w 肯定也会不同。因此,全连接层是必须确定输入,输出个数的)。
一张图图片会有大约 2k 个候选框,每一个都要单独输入 CNN 做卷积等操作很费时。SPP Net 提出:能否在 feature map 上提取 ROI 特征,这样就只需要在整幅图像上做一次卷积。SPP Net 在最后一个卷积层后,接入了金字塔池化层,使用这种方式,可以让网络输入任意的图片,而且还会生成固定大小的输出。
何凯明团队的 SPP Net 给出的解决方案是,既然只有全连接层需要固定的输入,那么我们在全连接层前加入一个网络层,让他对任意的输入产生固定的输出不就好了吗?一种常见的想法是对于最后一层卷积层的输出 pooling 一下,但是这个 pooling 窗口的尺寸及步伐设置为相对值,也就是输出尺寸的一个比例值,这样对于任意输入经过这层后都能得到一个固定的输出。SPP Net 在这个想法上继续加入 SPM 的思路,SPM 其实在传统的机器学习特征提取中很常用,主要思路就是对于一副图像分成若干尺度的一些块,比如一幅图像分成 1 份,4 份,8 份等。然后对于每一块提取特征然后融合在一起,这样就可以兼容多个尺度的特征啦。SPP Net 首次将这种思想应用在 CNN 中,对于卷积层特征我们也先给他分成不同的尺寸,然后每个尺寸提取一个固定维度的特征,最后拼接这些特征不就是一个固定维度的输入了吗?

所谓空间金字塔池化就是沿着金字塔的低端向顶端一层一层做池化。

上图的空间金字塔池化层是 SPP Net 的核心,其主要目的是对于任意尺寸的输入产生固定大小的输出。思路是对于任意大小的 feature map 首先分成 16、4、1 个块,然后在每个块上最大池化,池化后的特征拼接得到一个固定维度的输出。以满足全连接层的需要。不过因为不是针对于目标检测的,所以输入的图像为一整副图像。
假设原图输入是 224x224,对于 conv5 出来后的输出是 13x13x256 的,可以理解成有 256 个这样的 filter,每个 filter 对应一张 13x13 的 response map。如果像上图那样将 response map 分成 1x1(金字塔底座),2x2(金字塔中间),4x4(金字塔顶座)三张子图,分别做 max pooling 后,出来的特征就是 (16+4+1)x256 维度。如果原图的输入不是 224x224,出来的特征依然是 (16+4+1)x256 维度。这样就实现了不管图像尺寸如何池化 n 的输出永远是 (16+4+1)x256 维度。
实际运用中只需要根据全连接层的输入维度要求设计好空间金字塔即可。
网络细节
1. 卷积层特征图

SPP Net 通过可视化 conv5 层特征,发现卷积特征其实保存了空间位置信息(数学推理中更容易发现这点),并且每一个卷积核负责提取不同的特征,比如 C 图 175、55 卷积核的特征,其中 175 负责提取窗口特征,55 负责提取圆形的类似于车轮的特征。我们可以通过传统的方法聚集这些特征,例如词袋模型或是空间金字塔的方法。
2. 空间金字塔池化(Spatial Pyramid Pooling)
虽然总体流程还是 Selective Search 得到候选区域 —> CNN 提取ROI 特征 —> 类别判断 —> 位置精修,但是由于所有 ROI 的特征直接在 feature map 上提取,大大减少了卷积操作,提高了效率。
有两个难点要解决:
- 原始图像的 ROI 如何映射到特征图(feature map,一系列卷积层的最后输出)
- ROI 的在特征图上的对应的特征区域的维度不满足全连接层的输入要求怎么办(又不可能像在原始 ROI 图像上那样进行截取和缩放)?
对于难点 2:
- 这个问题涉及的流程主要有:图像输入
—>卷积层1—>池化1—>…—>卷积层n—>池化n—>全连接层。 - 引发问题的原因主要有:全连接层的输入维度是固定死的,导致池化
n的输出必须与之匹配,继而导致图像输入的尺寸必须固定。
为了使一些列卷积层的最后输出刚维度好是全连接层的输入维度,解决方法可能有:
- 想办法让不同尺寸的图像也可以使池化
n产生固定的 输出维度(打破图像输入的固定性) - 想办法让全连接层可以接受非固定的输入维度(打破全连接层的固定性,继而也打破了图像输入的固定性)
以上的方法 1 就是 SPP Net 的思想。它在池化 n 的地方做了一些手脚(特殊池化手段:空间金字塔池化),使得不同尺寸的图像也可以使池化 n 产生固定的输出维度。至于方法 2,其实就是全连接转换为全卷积,作用的效果等效为在原始图像做滑窗,多个窗口并行处理)
3. SPP Net应用于图像分类
SPP Net 的能够接受任意尺寸图片的输入,但是训练难点在于所有的深度学习框架都需要固定大小的输入,因此 SPP Net 做出了多阶段多尺寸训练方法。在每一个 epoch 的时候,我们先将图像放缩到一个 size,然后训练网络。训练完整后保存网络的参数,然后 resize 到另外一个尺寸,并在之前权值的基础上再次训练模型。相比于其他的 CNN 网络,SPP Net 的优点是可以方便地进行多尺寸训练,而且对于同一个尺度,其特征也是个空间金字塔的特征,综合了多个特征的空间多尺度信息。
4. SPP Net 应用于目标检测
SPP Net 理论上可以改进任何 CNN 网络,通过空间金字塔池化,使得 CNN 的特征不再是单一尺度的。但是 SPP Net 更适用于处理目标检测问题,首先是网络可以介绍任意大小的输入,也就是说能够很方便地多尺寸训练。其次是空间金字塔池化能够对于任意大小的输入产生固定的输出,这样使得一幅图片的多个 region proposal 提取一次特征成为可能。SPP Net 的做法是:
首先通过 selective search 产生一系列的 region proposal
然后训练多尺寸识别网络用以提取区域特征,其中处理方法是每个尺寸的最短边大小在尺寸集合中:
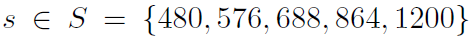
训练的时候通过上面提到的多尺寸训练方法,也就是在每个 epoch 中首先训练一个尺寸产生一个 model,然后加载这个 model 并训练第二个尺寸,直到训练完所有的尺寸。空间金字塔池化使用的尺度为:
1x1,2x2,3x3,6x6,一共是50个bins。
- 在测试时,每个 region proposal 选择能使其包含的像素个数最接近
224x224的尺寸,提取相 应特征。
由于我们的空间金字塔池化可以接受任意大小的输入,因此对于每个region proposal将其映射到feature map上,然后仅对这一块feature map进行空间金字塔池化就可以得到固定维度的特征用以训练CNN了。关于从region proposal映射到feature map的细节我们待会儿去说。
- 训练 SVM,bounding box 回归
5. 如何从一个 region proposal 映射到 feature map 的位置?
SPP Net 通过角点尽量将图像像素映射到 feature map 感受野的中央,假设每一层的 padding 都是 p/2(p为卷积核大小)。对于 feature map 的一个像素 (x',y'),其实际感受野为:(Sx‘,Sy’),其中 S 为之前所有层步伐的乘积。然后对于 region proposal 的位置,我们获取左上右下两个点对应的 feature map 的位置,然后取特征就好了。左上角映射为:
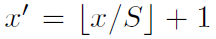
右下角映射为:
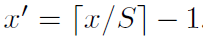
当然,如果 padding 大小不一致,那么就需要计算相应的偏移值啦。
金字塔池化的意义
总结而言,当网络输入的是一张任意大小的图片,这个时候可以一直进行卷积、池化,直到网络的倒数几层的时候,也就是即将与全连接层连接的时候,就要使用金字塔池化,使得任意大小的特征图都能够转换成固定大小的特征向量,这就是空间金字塔池化的意义(多尺度特征提取出固定大小的特征向量)。
SPP Net & RCNN
对于 RCNN,整个过程是:
- 首先通过 Selective Search,对待检测的图片进行搜索出大约
2000个候选窗口。 - 把这
2k个候选窗口的图片都缩放到227x227,然后分别输入 CNN 中,每个 proposal 提取出一个特征向量,也就是说利用 CNN 对每个 proposal 进行提取特征向量。 - 把上面每个候选窗口的对应特征向量,利用 SVM 算法进行分类识别。
可以看出 RCNN 的计算量是非常大的,因为 2k 个候选窗口都要输入到 CNN 中,分别进行特征提取。
而对于 SPP Net,整个过程是:
- 首先通过 Selective Search,对待检测的图片进行搜索出
2000个候选窗口。这一步和 RCNN 一样。 - 特征提取阶段。这一步就是和 RCNN 最大的区别了,这一步骤的具体操作如下:把整张待检测的图片,输入 CNN 中,进行一次性特征提取,得到 feature maps,然后在 feature maps 中找到各个候选框的区域,再对各个候选框采用金字塔空间池化,提取出固定长度的特征向量。而 RCNN 输入的是每个候选框,然后在进入 CNN,因为 SPP Net 只需要一次对整张图片进行特征提取,速度会大大提升。
- 最后一步也是和 RCNN 一样,采用 SVM 算法进行特征向量分类识别。
AlexNet
1. 模型结构

如上图所示,采用是两台GPU服务器,所有会有两个流程图。该模型一共分为 8 层——5 个卷积层,3 个全连接层(卷积层后面加了最大池化层),包含 6 亿 3000 万个连接,6000 万个参数和 65 万个神经元。在每一个卷积层中,包含了激励函数 ReLU 以及局部响应归一化(LRN)处理,然后再经过降采样(pooling 处理)。
2. 具体结构
整个网络共有 8 个需要训练的层,前 5 个为卷积层,最后 3 层为全连接层。
第一层:卷积层(conv1)
- 输入图片大小为:
224×224×3(经过预处理后实际大小变为227×227×3) - 卷积核:
11×11×3;步长:4;数量:96(图中为48个是由于采用了2` 个 GPU。由于卷积核的深度与图像深度一样,所以提取到的特征也是彩色的) - 卷积后的数据:
55×55×96【(227-11+1)/4 = 55(向上取整)】 relu1后的数据:55×55×96- 最大池化层
pool1的核:3×3;步长:2。因此输出的尺寸为:(227-11+1)/4 = 55(向上取整) pool1后的数据(降采样):27×27×96【(55-3+1)/2 = 27】- 局部归一化 LRN
norm1:local_size = 5(归一化运算的尺度为5×5) - 输出:
27×27×96。
第二层:卷积层(conv2)
- 输入数据:
27×27×96 - 卷积核:
5×5×96;步长:1;数量:256 - 卷积后的数据:
27×27×256(SAME padding,使得卷积后图像大小不变) relu2后的数据:27×27×256pool2的核(最大池化):3×3;步长:2pool2后的数据:13×13×256【(27-3+1)/2 = 13】norm2:local_size = 5- 输出:
13×13×256
第三层:卷积层(conv3)
- 输入数据:
13×13×256 - 卷积核:
3×3;步长:1;数量:384 - 卷积后数据:
13×13×384(SAME padding) relu3后的数据:13×13×384- 输出:
13×13×384
conv3 层没有 max pool 层和 norm 层。
第四层:卷积层(conv4)
- 输入数据:
13×13×384 - 卷积核:
3×3;步长:1;数量:384 - 卷积后数据:
13×13×384(SAME padding) relu4后的数据:13×13×384- 输出:
13×13×384
conv4 层也没有 max pool 层和 norm 层。
第五层:卷积层(conv5)
- 输入数据:
13×13×384 - 卷积核:
3×3;步长:1;数量:256 - 卷积后数据:
13×13×256(SAME padding) relu5后的数据:13×13×256pool5的核:3×3;步长:2pool5后的数据:6×6×256【(13-3+1)/2 = 6】- 输出:
6×6×256
conv5 层有 max pool,没有 norm 层
第六层:全连接层(fc6)
- 输入数据:
6×6×256 - 全连接输出:
4096×1 relu6后的数据:4096×1dropout6后数据:4096×1- 输出:
4096×1
第七层:全连接层(fc7)
- 输入数据:
4096×1 - 全连接输出:4096×1
relu7后的数据:4096×1dropout7后数据:4096×1- 输出:
4096×1
第八层:全连接层(fc8)
- 输入数据:
4096×1 - 全连接输出:
1000 - 输出一千种分类的概率
Alexnet 网络定义如下(alexnet_inference.py):
import tensorflow as tf
def print_layers(layer):
print(layer.op.name, ' ', layer.get_shape().as_list())
def inference(input_tensor, keep_prob, num_classes):
# conv1
with tf.name_scope('conv1'):
conv1_weights = tf.get_variable(
'weight1',
[11, 11, 3, 96],
initializer=tf.truncated_normal_initializer(stddev=0.1)
)
conv1_biases = tf.get_variable(
'bias1',
[96],
initializer=tf.constant_initializer(0.)
)
conv1 = tf.nn.conv2d(
input_tensor,
conv1_weights,
strides=[1, 4, 4, 1],
padding='VALID'
)
relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))
pool1 = tf.nn.max_pool(
relu1,
ksize=[1, 3, 3, 1],
strides=[1, 2, 2, 1],
padding='VALID'
)
norm1 = tf.nn.lrn(pool1, depth_radius=4, bias=1, alpha=1e-3/9, beta=0.75, name='norm1')
# conv2
with tf.name_scope('conv2'):
conv2_weights = tf.get_variable(
'weight2',
[5, 5, 96, 256],
initializer=tf.truncated_normal_initializer(stddev=0.1)
)
conv2_biases = tf.get_variable(
'bias2',
[256],
initializer=tf.constant_initializer(0.)
)
conv2 = tf.nn.conv2d(
norm1,
conv2_weights,
strides=[1, 1, 1, 1],
padding='SAME'
)
relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))
pool2 = tf.nn.max_pool(
relu2,
ksize=[1, 3, 3, 1],
strides=[1, 2, 2, 1],
padding='VALID'
)
norm2 = tf.nn.lrn(pool2, depth_radius=4, bias=1, alpha=1e-3/9, beta=0.75, name='norm1')
# conv3
with tf.name_scope('conv3'):
conv3_weights = tf.get_variable(
'weight3',
[3, 3, 256, 384],
initializer=tf.truncated_normal_initializer(stddev=0.1)
)
conv3_biases = tf.get_variable(
'bias3',
[384],
initializer=tf.constant_initializer(0.)
)
conv3 = tf.nn.conv2d(
pool2,
conv3_weights,
strides=[1, 1, 1, 1],
padding='SAME'
)
relu3 = tf.nn.relu(tf.nn.bias_add(conv3, conv3_biases))
# conv4
with tf.name_scope('conv4'):
conv4_weights = tf.get_variable(
'weight4',
[3, 3, 384, 384],
initializer=tf.truncated_normal_initializer(stddev=0.1)
)
conv4_biases = tf.get_variable(
'bias4',
[384],
initializer=tf.constant_initializer(0.)
)
conv4 = tf.nn.conv2d(
relu3,
conv4_weights,
strides=[1, 1, 1, 1],
padding='SAME'
)
relu4 = tf.nn.relu(tf.nn.bias_add(conv4, conv4_biases))
# conv5
with tf.name_scope('conv5'):
conv5_weights = tf.get_variable(
'weight5',
[3, 3, 384, 256],
initializer=tf.truncated_normal_initializer(stddev=0.1)
)
conv5_biases = tf.get_variable(
'bias5',
[256],
initializer=tf.constant_initializer(0.)
)
conv5 = tf.nn.conv2d(
relu4,
conv5_weights,
strides=[1, 1, 1, 1],
padding='SAME'
)
relu5 = tf.nn.relu(tf.nn.bias_add(conv5, conv5_biases))
pool5 = tf.nn.max_pool(
relu5,
ksize=[1, 3, 3, 1],
strides=[1, 2, 2, 1],
padding='VALID'
)
# fc6
with tf.name_scope('fc6'):
flattened = tf.reshape(pool5, shape=[-1, 6*6*256])
weights = tf.Variable(tf.truncated_normal(
[6*6*256, 4096],
dtype=tf.float32,
stddev=1e-1), name='weights')
biases = tf.Variable(tf.constant(0., shape=[4096], dtype=tf.float32),
name='biases')
relu6 = tf.nn.relu(tf.nn.xw_plus_b(flattened, weights, biases))
dropout6 = tf.nn.dropout(relu6, keep_prob)
# fc7
with tf.name_scope('fc7'):
weights = tf.Variable(tf.truncated_normal(
[4096, 4096],
dtype=tf.float32,
stddev=1e-1), name='weights')
biases = tf.Variable(tf.constant(0., shape=[4096], dtype=tf.float32),
name='biases')
relu7 = tf.nn.relu(tf.nn.xw_plus_b(dropout6, weights, biases))
dropout7 = tf.nn.dropout(relu7, keep_prob)
with tf.name_scope('fc8'):
weights = tf.Variable(tf.truncated_normal(
[4096, num_classes],
dtype=tf.float32,
stddev=1e-1), name='weights')
biases = tf.Variable(tf.constant(0., shape=[num_classes], dtype=tf.float32),
name='biases')
fc8 = tf.nn.xw_plus_b(dropout7, weights, biases)
return fc8
Alexnet 网络的训练过程(alexnet_train.py):
import os
import numpy as np
import tensorflow as tf
import alexnet_inference
import glob
from datetime import datetime
# 配置神经网络的参数
TRAIN_BATCH_SIZE = 10
TEST_BATCH_SIZE = 10
LEARNING_RATE = 1e-3
DROPOUT_RATE = 0.25
NUM_CLASSES = 2 # 类别标签
NUM_EPOCHS = 10
# 模型保存的路径和文件名
MODEL_SAVE_PATH = "model/"
MODEL_NAME = "model.ckpt"
TENSORBOARD_PATH = "tensorboard/" # 存储tensorboard文件
TOTAL_DATASET = 'train/'
TRAIN_DATASET_PATH = ['train/cat/',
'train/dog/']
TEST_DATASET_PATH = ['test/']
LABEL = ['cat',
'dog']
# 将图像转换为三维数据,将标签转换为one-hot形式
def parse_image(file_name, label):
image_string = tf.read_file(file_name)
image_decoded = tf.image.decode_jpeg(image_string, channels=3)
image_resized = tf.image.resize_images(image_decoded, [227, 227]) # 将图片居中
image_centered = tf.subtract(image_resized, [123.68, 116.779, 103.939])
image = image_centered[:, :, ::-1] # 将RGB转换为BGR
label = tf.one_hot(label, NUM_CLASSES)
return image, label
# 打乱图片顺序
def shuffle_images(train_images, train_labels):
permutation = np.random.permutation(len(train_labels))
images = []
labels = []
for i in permutation:
images.append(train_images[i])
labels.append(train_labels[i])
return images, labels
# 将图片和标签先转化为tensor,再创建Dataset,
def process_image(train_images, train_labels):
image_num = len(train_images)
train_images = tf.convert_to_tensor(train_images, dtype=tf.string)
train_labels = tf.convert_to_tensor(train_labels, dtype=tf.int32)
dataset = tf.data.Dataset.from_tensor_slices((train_images, train_labels))
dataset = dataset.map(parse_image).batch(TRAIN_BATCH_SIZE)
return dataset, image_num
def train():
if not os.path.isdir(MODEL_SAVE_PATH):
os.mkdir(MODEL_SAVE_PATH)
if not os.path.isdir(TOTAL_DATASET):
os.mkdir(TOTAL_DATASET)
if not os.path.isdir(list(TRAIN_DATASET_PATH)[0]) or not os.path.isdir(list(TRAIN_DATASET_PATH)[1]):
os.mkdir(list(TRAIN_DATASET_PATH)[0])
os.mkdir(list(TRAIN_DATASET_PATH)[1])
# 处理训练集图片
train_images = []
train_labels = []
for path in TRAIN_DATASET_PATH:
train_images[len(train_images): len(train_images)] = np.array(glob.glob(path + '*jpg')).tolist()
for path in train_images:
# file_name表示文件名
file_name = path.split('/')[-1]
for i in range(NUM_CLASSES):
if LABEL[i] in file_name:
train_labels.append(i)
break
train_images, train_labels = shuffle_images(train_images, train_labels)
train_data, train_data_size = process_image(train_images, train_labels)
# 将training的过程分为train_batches_per_epoch次迭代完成,每次迭代包含的元素为TRAIN_BATCH_SIZE个
train_batches_per_epoch = int(np.floor(train_data_size) / TRAIN_BATCH_SIZE)
train_iterator = tf.data.Iterator.from_structure(train_data.output_types, train_data.output_shapes)
train_initializer = train_iterator.make_initializer(train_data) # 创建dataset迭代器,需要进行初始化
train_next_batch = train_iterator.get_next()
# 处理测试集图片
test_images = []
test_labels = []
for path in TEST_DATASET_PATH:
test_images[len(test_images): len(test_images)] = np.array(glob.glob(path + '*jpg')).tolist()
for path in test_images:
# file_name表示文件名
file_name = path.split('/')[-1]
for i in range(NUM_CLASSES):
if LABEL[i] in file_name:
test_labels.append(i)
break
test_images, test_labels = shuffle_images(test_images, test_labels)
test_data, test_data_size = process_image(test_images, test_labels)
# 将training的过程分为train_batches_per_epoch次迭代完成,每次迭代包含的元素为TRAIN_BATCH_SIZE个
test_batches_per_epoch = int(np.floor(test_data_size) / TEST_BATCH_SIZE)
test_iterator = tf.data.Iterator.from_structure(test_data.output_types, test_data.output_shapes)
test_initializer = test_iterator.make_initializer(test_data) # 创建dataset迭代器,需要进行初始化
test_next_batch = test_iterator.get_next()
x = tf.placeholder(tf.float32, [None, 227, 227, 3])
y_ = tf.placeholder(tf.float32, [None, NUM_CLASSES])
keep_prob = tf.placeholder(tf.float32)
y = alexnet_inference.inference(x, keep_prob, NUM_CLASSES)
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=y, labels=y_))
train_op = tf.train.AdamOptimizer(LEARNING_RATE).minimize(loss)
accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)), tf.float32))
init_op = tf.global_variables_initializer()
# tensorboard
# tf.summary.scalar('loss,')
saver = tf.train.Saver()
with tf.Session() as sess:
sess.run(init_op)
print('{}: Start training...'.format(datetime.now()))
for epoch in range(NUM_EPOCHS):
sess.run(train_initializer)
print('ecpoch number: {} start'.format(epoch+1))
# train
# 200 / 10 = 20
for step in range(train_batches_per_epoch):
image_batch, label_batch = sess.run(train_next_batch)
loss_value, train_step = sess.run([loss, train_op], feed_dict={
x: image_batch,
y_: label_batch,
keep_prob: DROPOUT_RATE
})
if step % 10 ==0:
print("After %d training step(s), loss on training batch is %f." % (epoch, loss_value))
# accuracy
sess.run(test_initializer)
test_accuracy = 0
test_count = 0
for _ in range(test_batches_per_epoch):
image_batch, label_batch = sess.run(test_next_batch)
temp_accuracy = sess.run(accuracy, feed_dict={x: image_batch,
y_: label_batch,
keep_prob: 1.0})
test_accuracy += temp_accuracy
test_count += 1
try:
test_accuracy /= test_count
except:
print('ZeroDivisionError!')
print("Accuracy = {:.4f}".format(test_accuracy))
# save model
print("{}: Saving model... ".format(datetime.now()))
saver.save(sess, os.path.join(MODEL_SAVE_PATH,MODEL_NAME), global_step=epoch)
def main(argv=None):
train()
main()
# if __name__ == '__main__':
# tf.app.run()
3. 创新点
1. ReLU Nonlinearity
一般神经元的激活函数会选择 sigmoid 函数或者 tanh 函数,然而 Alex 发现在训练时间的梯度衰减方面,这些非线性饱和函数要比非线性非饱和函数慢很多。在 AlexNet 中用的非线性非饱和函数是 f=max(0,x),即 ReLU。实验结果表明,要将深度网络训练至 training error rate 达到 25% 的话,ReLU 只需 5 个 epochs 的迭代,但 tanh 需要 35 个 epochs 的迭代,用 ReLU 比 tanh 快 6 倍。
2. 双 GPU 并行运行
为提高运行速度和提高网络运行规模,采用双 GPU 的设计模式。并且规定 GPU只能在特定的层进行通信交流。其实就是每一个 GPU 负责一半的运算处理。值得注意的是,虽然 one-GPU 网络规模只有 two-GPU 的一半,但其实这两个网络其实并非等价的。
3. LRN 局部响应归一化
ZF Net
源自论文《Visualizing and Understanding Convolutional Networks 》
1. 概述
本文设计了一种可以可视化卷积层中 feature map 的系统,通过可视化每层 layer 的某些 activation 来探究 CNN 网络究竟是怎样“学习”的,同时文章通过可视化了 AlexNet 发现了因为结构问题,导致有“影像重叠”(aliasing artifacts),因此对网络进行了改进,设计出了 ZF Net。
文章通过把 activation(feature map 中的数值)映射回输入像素的空间,去了解什么样的输入模式会生成 feature map 中的一个给定activation,这个模型主要通过反卷积(deconvolution),反向池化(Unpooling)与“反向激活”(Rectification),其实就是把整个 CNN 网络倒过来,另外值得说一下的是,并不是完全倒过来,只是近似,所有的“反向”操作都是近似,主要是使得从各层 layer 的尺度还原到在原始图像中相应大小的尺度。
同时文章还分析了每层 layer 学习到了什么,以及可视化最强 activation 的演化过程来关系模型的收敛过程,同时也利用遮挡某些部位来学习 CNN 是学习 object 本身还是周围环境。
2. 可视化结构
2.1 Unpooling
要想完全还原 max pooling 是不太现实的,除非记录每一层 feature,那有些得不偿失,文章通过记录池化过程中最大激活值所在位置以及数值,在 unpooling 的时候,还原那个数值,其他的位置设为 0,从而近似“反向池化”,具体如下图:

2.2 Rectification
CNN 使用 ReLU 确保每层输出的激活之都是正数,因此对于反向过程,同样需要保证每层的特征图为正值,也就是说这个反激活过程和激活过程没有什么差别,都是直接采用 ReLU 函数。
2.3 Filtering
卷积过程使用学习到的过滤器对 feature map 进行卷积,为近似反转这个过程,反卷积使用该卷积核的转置来进行卷积操作。
注意:在上述重构过程中没有使用任何对比度归一化操作
3. Feature Visualization
在 ImageNet 验证集上使用反卷积进行特征图的可视化,如下图:



对于一个给定的 feature map,展示了响应最大的九张响应图,每个响应图向下映射到原图像素空间,右面的原图通过找到在原图的感受野来截取对应的原图。
通过观察可以发现,来自每个层中的投影显示出网络中特征的分层特性。第二层响应角落和其他的边缘/颜色信息,层三具有更复杂的不变性,捕获相似的纹理,层四显示了显著的变化,并且更加类别具体化,层五则显示了具有显著姿态变化的整个对象,所以这就是常说的 CNN 结构前几层通常学习简单的线条纹理,一些共性特征,后面将这些特征组合成 不同的更丰富的语义内容。
4. Feature Evolution during Training
文中对于一个 layer 中给定的 feature map,图中给出在训练 epochs 在 [1,2,5,10,20,30,40,64]时,训练集对该 feature map 响应最大的可视化图片,如下图:

从图中可以看出,较低层 (L1, L2) 只需要几个 epochs 就可以完全收敛,而高层 (L5) 则需要很多次迭代,需要让模型完全收敛之后。这一点正好与深层网络的梯度弥散现象正好相反,但是这种底层先收敛,然后高层再收敛的现象也很符合直观。
5. Feature Invariance

上图显示出了相对于未变换的特征,通过垂直平移,旋转和缩放的 5 个样本图像在可视化过程中的变化。小变换对模型的第一层有着显著的影响,但对顶层影响较小,对于平移和缩放是准线性的。网络输出对于平移和缩放是稳定的。但是一般来说,除了具有旋转对称性的物体来说,输出来旋转来说是不稳定的(这说明了卷积操作对于平移和缩放具有很好的不变性,而对于旋转的不变性较差)。
6. ZF Net

可视化训练模型不但可以洞察 CNN 的操作,也可以帮助我们在前几层选择更好的模型架构。通过可视化 AlexNet 的前两层(图中b,d),就可以看出问题:
- 第一层 filter 是非常高频和低频的信息,中间频率的filter很少覆盖
- 第二层的可视化有些具有混叠效应,由于第一层比较大的 stride
为了解决这些问题:
将第一层的 filter 的尺寸从
11x11减到7x7缩小间隔,从
4变为2。
这两个改动形成的新结构,获取了更多的信息,而且提升了分类准确率。
7. 实验
首先,作者进行了网络结构尺寸调整实验。去除掉包含大部分网络参数最后两个全连接层之后,网络性能下降很少;去掉中间两层卷积层之后,网络性能下降也很少;但是当把上述的全连接层和卷积层都去掉之后,网络性能急剧下降,由此作者得出结论:模型深度对于模型性能很重要,存在一个最小深度,当小于此深度时,模型性能大幅下降。
作者固定了通过 ImageNet pre-train 网络的权值,只是使用新数据训练了 softmax 分类器,效果非常好。这就形成了目前的人们对于卷积神经网络的共识:卷积网络相当于一个特征提取器。特征提取器是通用的,因为 ImageNet 数据量,类别多,所以由 ImageNet 训练出来的特征提取器更具有普遍性。也正是因为此,目前的卷积神经网络的 Backbone Network 基本上都是 ImageNet 上训练出来的网络。
总结
本文最大的贡献在于通过使用可视化技术揭示了神经网络各层到底在干什么,起到了什么作用。可视化技术依赖于反卷积操作,即卷积的逆过程,将特征映射到像素上。具体过程如下图所示:
- Unpooling:在卷积神经网络中,最大池化是不可逆的,作者采用近似的实现,使用一组转换变量 switch 记录每个池化区域最大值的位置。在反池化的时候,将最大值返回到其所应该在的位置,其他位置用
0补充。 - Rectification:反卷积的时候也同样利用 ReLU 激活函数
- Filtering:解卷积网络中利用卷积网络中相同的 filter 的转置应用到 Rectified Unpooled Maps,也就是对 filter 进行水平方向和垂直方向的翻转。

可视化不仅能够看到一个训练完的模型的内部操作,而且还能够帮助改进网络结构从而提高网络性能。ZF Net 模型是在 AlexNet 基础上进行改动,网络结构上并没有太大的突破。差异表现在,AlexNet 是用两块 GPU 的稀疏连接结构,而 ZF Net 只用了一块 GPU 的稠密链接结构;改变了 AlexNet 的第一层,将过滤器的大小由 11x 11 变成 7x7,并且将步长由 4 变成 2 ,使用更小的卷积核和步长,保留更多特征;将3,4,5 层变成了全连接。

VGG Net
出自论文 《Very Deep Convolutional Networks for Large-Scale Image Recognition》
1. 概括
VGG 模型由牛津大学 VGG 组提出。VGG 全部使用了 3x3 的卷积核和 2x2 最大池化核通过不断加深网络结构来提神性能。采用堆积的小卷积核优于采用大的卷积核,因为多层非线性层可以增加网络深层来保证学习更复杂的模式,而且所需的参数还比较少。
VGG 论文给出了一个非常振奋人心的结论:卷积神经网络的深度增加和小卷积核的使用对网络的最终分类识别效果有很大的作用。
2. 创新点
VGG 全部使用 3x3 的卷积核和 2x2 的池化核,通过不断加深网络结构来提升性能。网络层数的增长并不会带来参数量上的爆炸,因为参数量主要集中在最后三个全连接层中。同时,两个 3x3 卷积层的串联相当于 1 个 5x5 的卷积层(在像素关联性上,两个 3x3 的卷积可连接到范围与一个 5x5 卷积可连接到的范围相当),3 个 3x3 的卷积层串联相当于 1 个 7x7 的卷积层,即 3 个 3x3 卷积层的感受野大小相当于 1 个 7x7 的卷积层。但是 3 个 3x3 的卷积层参数量只有 7x7 的一半左右,同时前者可以有 3 个非线性操作,而后者只有 1 个非线性操作,这样使得前者对于特征的学习能力更强。

使用 1x1 的卷积层来增加线性变换,输出的通道数量上并没有发生改变。这里提一下 1x1 卷积层的其他用法,1x1 的卷积层常被用来提炼特征,即多通道的特征组合在一起,凝练成较大通道或者较小通道的输出,而每张图片的大小不变。有时 1x1 的卷积神经网络还可以用来替代全连接层。
VGG 在训练的时候先训级别 A 的简单网络,再复用 A 网络的权重来初始化后面的几个复杂模型,这样收敛速度更快。VGG 作者总结出 LRN 层作用不大,越深的网络效果越好,1x1 的卷积也是很有效的,但是没有 3x3 的卷积效果好,因为 3x3 的网络可以学习到更大的空间特征。
3. VGG 网路结构:
网络的输入为 224x224的 RGB 图片,后面跟卷积层,卷积核的大小基本都为 3x3 ,这一种最小的、可以保留图片空间分辨率的卷积核,步长为 1 个像素,偶尔会有 1x1 的卷积核,这就相当于加入了一个非线性变换而已。再往后接 pooling 层,它的大小为 2x2,步长为 2 个像素,并且采用 max pooling 的方法;再往后就是三层的全连层,第一层为 4096 个单元,第二层为 4096 个单元,第三层为 1000 个单元,即对应 1000 个类别,根据这 1000 个单元的输出其实这样就可以分类了;再往后为一个 softmax 层,目的其实就是用于计算网络的代价函数时用于求误差。
VGG 的网络结构如下图所示。VGG 包含很多级别的网络,深度从 11 层到 19 层不等,比较常用的是 VGG-16 和 VGG-19。VGG 把网络分成了 5 段,每段都把多个 3x3 的卷积网络串联在一起,每段卷积后面接一个最大池化层,最后面是 3 个全连接层和一个 softmax 层。

在上图中,如网络中的 conv3-512,表示网络的卷积核的大小为 3x3, 共有 512 个 feature map。另外,max pool 的具体配置没有写出来。
VGG 网络参数( 下图是整个模型的参数总量,单位是 millions,参数来自卷积层和全连接层,主要是全连接层):

- 两个堆叠的卷积层(卷积核为
3x3)有限感受野是5x5,三个堆叠的卷积层(卷积核为3x3)的感受野为7x7,故可以堆叠含有小尺寸卷积核的卷积层来代替具有大尺寸的卷积核的卷积层,并且能够使得感受野大小不变,而且多个3x3的卷积核比一个大尺寸卷积核有更多的非线性(每个堆叠的卷积层中都包含激活函数),使得 decision function更加具有判别性。 - 假设一个
3层的3x3卷积层的输入和输出都有Cchannels,堆叠的卷积层的参数个数为,而等同的一个单层的
7x7卷积层的参数为
可以看到 VGG-D 使用了一种块结构:多次重复使用统一大小的卷积核来提取更复杂和更具有表达性的特征。VGG 系列中,最多使用是 VGG-16,下图来自 Andrew Ng 深度学习里面对 VGG-16 架构的描述。如图所示,在 VGG-16 的第三、四、五块:256、512、512 个过滤器依次用来提取复杂的特征,其效果就等于一个带有3各卷积层的大型 512x512 大分类器。

4. 训练
4.1 训练初始化参数
VGG 采用了 min-batch gradient descent 去优化 multinomial logistic regression objective:
batch size:256momentum:0.9learning_rate:1e−2(训练过程中,降低了三次,每次减少0.1)max iterations:370K次迭代,74epochs
正则化方法:
- 增加了对权重的正则化:

- 对 FC 全连接层进行 dropout 正则化,
dropout ratio = 0.5
说明:虽然模型的参数和深度相比 AlexNet 有了很大的增加,但是模型的训练迭代次数却要求更少,这是因为:
- 正则化 + 小卷积核
- 特定层的预初始化
初始化策略(VGG 在训练时用到的 track):
首先,随机初始化网络结构
A(A的深度较浅)利用
A的网络参数,给其他的模型进行初始化(初始化前4层卷积 + 全连接层,其他的层采用正态分布随机初始化,mean=0,variance=1e−2,biases = 0,即均值为0,方差为1e-2)
简而言之,就是先训练级别 A 的简单网络,再复用 A 网络的权重来初始化后面的几个复杂模型,这样训练收敛的速度更快。最后证明,即使随机初始化所有的层,模型也能训练的很好
4.2 训练输入
采用随机裁剪的方式,获取固定大小 224x224 的输入图像,并且采用了随机水平镜像和随机平移图像通道来丰富数据。
- Training image size:令
S为图像的最小边,如果最小边S=224,则直接在图像上进行224x224区域随机裁剪,这时相当于裁剪后的图像能够几乎覆盖全部的图像信息;如果最小边S>>224,那么做完224x224区域随机裁剪后,每张裁剪图,只能覆盖原图的一小部分内容【注:因为训练数据的输入为224x224,从而图像的最小边S,不应该小于224】 - 数据生成方式:首先对图像进行放缩变换,将图像的最小边缩放到
S大小,然后:- 方法 1:在
S=224和S=384的尺度下,对图像进行224x224区域随机裁剪 - 方法 2:令
S随机的在 区间内值,放缩完图像后,再进行随机裁剪(其中
区间内值,放缩完图像后,再进行随机裁剪(其中 ,
, )
)
- 方法 1:在
- 预测(作者考虑了两种预测方式):
- 方法 1:multi-crop,即对图像进行多样本的随机裁剪,然后通过网络预测每一个样本的结构,最终对所有结果平均
- 方法 2:densely, 利用 FCN 的思想,将原图直接送到网络进行预测,将最后的全连接层改为
1x1的卷积,这样最后可以得出一个预测的 score map,再对结果求平均 - 对于上述这两种方法:
- multi-crops 相对于 FCN 效果要好
- multi-crops 相当于对于 dense evaluation 的补充,原因在于,两者在边界的处理方式不同:multi-crop 相当于 padding 补充
0值,而 dense evaluation 相当于 padding 补充了相邻的像素值,并且增大了感受野 - multi-crop 存在重复计算带来的效率的问题
在预测时,VGG 采用 Multi-Scale 的方法:即将图像 scale 到一个尺寸 Q,并将图片输入卷积网络计算。然后在最后一个卷积层使用滑窗的方式进行分类预测,将不同窗口的分类结果平均,再将不同尺寸 Q 的结果平均得到最后结果,这样可提高图片数据的利用率并提升预测准确率。在训练中,VGG 还使用 Multi-Scale 的方法做数据增强,将原始图像缩放到不同尺寸 S,然后再随机裁切 224x224 的图片,这样能增加很多数据量,对于防止模型过拟合有很不错的效果。实践中,作者令 S 在 [256, 512] 这个区间内取值,使用 Multi-Scale 获得多个版本的数据,并将多个版本的数据合在一起进行训练。
5. 实验效果(CLASSIFICATION EXPERIMENTS )
5.1 单尺度(SINGLE SCALE EVALUATION )

结论:
- 模型 E(VGG19)的效果最好,即网络越深,效果越好
- 同一种模型,随机 scale jittering 的效果好于固定
S大小的256,384两种尺度,即 scale jittering ( )数据增强能更准确的提取图像多尺度信息
)数据增强能更准确的提取图像多尺度信息
5.2 多尺度(MULTI-SCALE EVALUATION )
下图为 VGG 使用 Multi-Scale 训练时得到的结果,可以看到 D 和 E 都可以达到 7.5% 的错误率。最终提交到 ILSVRC 2014 的版本是仅使用 Single-Scale 的 6 个不同等级的网络与 Multi-Scale 的 D 网络的融合,达到了 7.3% 的错误率。不过比赛结束后作者发现只融合 Multi-Scale 的 D 和 E 可以达到更好的效果,错误率达到 7.0%,再使用其他优化策略最终错误率可达到 6.8% 左右,非常接近同年的冠军Google Inception-Net。

结论:
- 对比单尺度预测,多尺度综合预测能够提升预测的精度
- 同单尺度预测,多尺度预测也证明了 scale jittering 的作用
5.3 多尺度裁剪(MULTI-CROP EVALUATION )

结论:
- 数据生成方式 multi-crop 效果略优于 dense,但作者上文也提高,精度的提高不足以弥补计算上的损失
- multi-crop于dense 方法结合的效果最后,也证明了作者的猜想:multi-crop和dense两种方法互为补充
同时,作者在对比各级网络时总结出了以下几个观点:
- LRN 层作用不大(VGG 不使用局部响应标准化,这种标准化并不能在 ILSVRC 数据集上提升性能,却导致更多的内存消耗和计算时间)
- 越深的网络效果越好
1x1的卷积也是很有效的,但是没有3x3的卷积好,大一些的卷积核可以学习更大的空间特征。
在训练的过程中,比 AlexNet 收敛的要快一些,原因为:
- 使用小卷积核和更深的网络进行的正则化
- 在特定的层使用了预训练得到的数据进行参数的初始化。
对于较浅的网络,如网络 A,可以直接使用随机数进行随机初始化,而对于比较深的网络,则使用前面已经训练好的较浅的网络中的参数值对其前几层的卷积层和最后的全连接层进行初始化。
5.4 网络融合(CONVNET FUSION)
其实就是多个网络模型的输出结果求平均再用于识别。在 ILSVRC 的比赛中大家都在用,为什么呢?因为这样做基本上稍微弄弄,都可以提高网络的识别率。原理可能就是所谓的不同网络模型之间的互补(complementarity,这也说明了网络的不稳定吧)。
6. Q&A
Q1: 为什么 3 个 3x3 的卷积可以代替 7x7 的卷积?
3个3x3的卷积,使用了3个非线性激活函数,增加了非线性表达能力,使得分割平面更具有可分性- 减少了参数个数。对于
C个通道的卷积核,7x7含有参数 ,参数大大减少
Q2:2 个 3x3 卷积核可以来代替 5x5 卷积核?
5x5 卷积看做一个小的全连接网络在 5x5 区域滑动,我们可以先用一个 3x3 的卷积滤波器卷积,然后再用一个全连接层连接这个 3x3 卷积输出,这个全连接层我们也可以看做一个 3x3 卷积层。这样我们就可以用两个 3x3 卷积级联(叠加)起来代替一个 5x5 卷积。
具体如下图所示:

Q3: 1x1 卷积核的作用?
在不影响感受野的情况下,增加模型的非线性性
1x1卷积相当于线性变换,非线性激活函数起到非线性作用
Q4: 网络深度对结果的影响(同年 google 也独立发布了深度为 22 层的网络 GoogleNet)
- VGG 与 GoogleNet 模型都很深
- 都采用了小卷积
- VGG 只采用
3x3,而 GoogleNet 采用1x1,3x3,5x5,模型更加复杂(模型开始采用了很大的卷积核,来降低后面卷机层的计算)
7. VGG TensorFlow 实现
7.1 自己实现
import tensorflow as tf
from tensorflow.contrib.layers import xavier_initializer_conv2d
from tensorflow.contrib.layers import flatten
# 定义卷积层
def conv(input_tensor, fileter_size, out_channels, step, name):
in_channels = input_tensor.get_shape()[-1].value
with tf.name_scope(name) as scope:
weights = tf.get_variable(
shape=[fileter_size, fileter_size, in_channels, out_channels],
dtype=tf.float32,
initializer=xavier_initializer_conv2d(),
name=scope+'weights')
biases = tf.Variable(
tf.constant(value=0., shape=[out_channels], dtype=tf.float32),
trainable=True,
name='biases')
relu = tf.nn.relu(tf.nn.bias_add(tf.nn.conv2d(input_tensor,
weights,
strides=[1, step, step, 1],
padding='SAME'),
biases),
name=scope)
return relu
# 最大池化
def max_pool(input_tensor, fileter_size, step, name):
return tf.nn.max_pool(
input_tensor,
ksize=[1, fileter_size, fileter_size, 1],
strides=[1, step, step, 1],
padding='SAME',
name=name)
# 全连接层
def fc(input_tensor, out_channels, name):
in_channels = input_tensor.get_shape()[-1].value
with tf.name_scope(name) as scope:
weights = tf.get_variable(
shape=[in_channels, out_channels],
dtype=tf.float32,
initializer=xavier_initializer_conv2d(),
name=scope+'weights')
biases = tf.Variable(
tf.constant(value=0., shape=[out_channels], dtype=tf.float32),
name='biases')
relu = tf.nn.relu_layer(input_tensor, weights, biases, name=scope)
return relu
# 定义 VGG-16 网络
def vgg_16(images, keep_prob):
# 第一个块结构,包括两个con3-64
with tf.name_scope('block_1'):
conv1_1 = conv(images, fileter_size=3, out_channels=64, step=1, name='conv1_1')
conv1_2 = conv(conv1_1, fileter_size=3, out_channels=64, step=1, name='conv1_2')
pool1 = max_pool(conv1_2, fileter_size=2, step=2, name='pooling_1')
# 第二个块结构,包括两个con3-128
with tf.name_scope('block_2'):
conv2_1 = conv(pool1, fileter_size=3, out_channels=128, step=1, name='conv2_1')
conv2_2 = conv(conv2_1, fileter_size=3, out_channels=128, step=1, name='conv2_2')
pool2 = max_pool(conv2_2, fileter_size=2, step=2, name='pooling_2')
# 第三个块结构,包括两个con3-256
with tf.name_scope('block_3'):
conv3_1 = conv(pool2, fileter_size=3, out_channels=256, step=1, name='conv3_1')
conv3_2 = conv(conv3_1, fileter_size=3, out_channels=256, step=1, name='conv3_2')
conv3_3 = conv(conv3_2, fileter_size=3, out_channels=256, step=1, name='conv3_3')
pool3 = max_pool(conv3_3, fileter_size=2, step=2, name='pooling_3')
# 第四个块结构,包括两个con3-512
with tf.name_scope('block_4'):
conv4_1 = conv(pool3, fileter_size=3, out_channels=512, step=1, name='conv4_1')
conv4_2 = conv(conv4_1, fileter_size=3, out_channels=512, step=1, name='conv4_2')
conv4_3 = conv(conv4_2, fileter_size=3, out_channels=512, step=1, name='conv4_3')
pool4 = max_pool(conv4_3, fileter_size=2, step=2, name='pooling_4')
# 第五个块结构,包括两个con3-512
with tf.name_scope('block_3'):
conv5_1 = conv(pool4, fileter_size=3, out_channels=512, step=1, name='conv5_1')
conv5_2 = conv(conv5_1, fileter_size=3, out_channels=512, step=1, name='conv5_2')
conv5_3 = conv(conv5_2, fileter_size=3, out_channels=512, step=1, name='conv5_3')
pool5 = max_pool(conv5_3, fileter_size=2, step=2, name='pooling_5')
# flatten
flattened = flatten(pool5)
dim = flattened.shape[1].value
with tf.name_scope('fc1_4096'):
fc1 =fc(flattened, out_channels=4096, name='fc1_4096')
fc1_drop = tf.nn.dropout(fc1, keep_prob=keep_prob, name='fc1_drop')
with tf.name_scope('fc2_4096'):
fc2 =fc(fc1_drop, out_channels=4096, name='fc2_4096')
fc2_drop = tf.nn.dropout(fc2, keep_prob=keep_prob, name='fc2_drop')
with tf.name_scope('fc_1000'):
fc3 =fc(fc2_drop, out_channels=1000, name='fc_1000')
logits = tf.nn.softmax(fc3)
return logits
7.2 Google 官方 slim 实现
import tensorflow as tf
slim = tf.contrib.slim
def vgg_arg_scope(weight_decay=0.0005):
with slim.arg_scope([slim.conv2d, slim.fully_connected],
activation_fn=tf.nn.relu,
weights_regularizer=slim.l2_regularizer(weight_decay),
biases_initializer=tf.zeros_initializer()):
with slim.arg_scope([slim.conv2d], padding='SAME') as arg_sc:
return arg_sc
def vgg_a(inputs,
num_classes=1000,
is_training=True,
dropout_keep_prob=0.5,
spatial_squeeze=True,
scope='vgg_a',
fc_conv_padding='VALID',
global_pool=False):
with tf.variable_scope(scope, 'vgg_a', [inputs]) as sc:
end_points_collection = sc.original_name_scope + '_end_points'
# Collect outputs for conv2d, fully_connected and max_pool2d.
with slim.arg_scope([slim.conv2d, slim.max_pool2d],
outputs_collections=end_points_collection):
net = slim.repeat(inputs, 1, slim.conv2d, 64, [3, 3], scope='conv1')
net = slim.max_pool2d(net, [2, 2], scope='pool1')
net = slim.repeat(net, 1, slim.conv2d, 128, [3, 3], scope='conv2')
net = slim.max_pool2d(net, [2, 2], scope='pool2')
net = slim.repeat(net, 2, slim.conv2d, 256, [3, 3], scope='conv3')
net = slim.max_pool2d(net, [2, 2], scope='pool3')
net = slim.repeat(net, 2, slim.conv2d, 512, [3, 3], scope='conv4')
net = slim.max_pool2d(net, [2, 2], scope='pool4')
net = slim.repeat(net, 2, slim.conv2d, 512, [3, 3], scope='conv5')
net = slim.max_pool2d(net, [2, 2], scope='pool5')
# Use conv2d instead of fully_connected layers.
net = slim.conv2d(net, 4096, [7, 7], padding=fc_conv_padding, scope='fc6')
net = slim.dropout(net, dropout_keep_prob, is_training=is_training,
scope='dropout6')
net = slim.conv2d(net, 4096, [1, 1], scope='fc7')
# Convert end_points_collection into a end_point dict.
end_points = slim.utils.convert_collection_to_dict(end_points_collection)
if global_pool:
net = tf.reduce_mean(net, [1, 2], keep_dims=True, name='global_pool')
end_points['global_pool'] = net
if num_classes:
net = slim.dropout(net, dropout_keep_prob, is_training=is_training,
scope='dropout7')
net = slim.conv2d(net, num_classes, [1, 1],
activation_fn=None,
normalizer_fn=None,
scope='fc8')
if spatial_squeeze:
net = tf.squeeze(net, [1, 2], name='fc8/squeezed')
end_points[sc.name + '/fc8'] = net
return net, end_points
vgg_a.default_image_size = 224
def vgg_16(inputs,
num_classes=1000,
is_training=True,
dropout_keep_prob=0.5,
spatial_squeeze=True,
scope='vgg_16',
fc_conv_padding='VALID',
global_pool=False):
with tf.variable_scope(scope, 'vgg_16', [inputs]) as sc:
end_points_collection = sc.original_name_scope + '_end_points'
# Collect outputs for conv2d, fully_connected and max_pool2d.
with slim.arg_scope([slim.conv2d, slim.fully_connected, slim.max_pool2d],
outputs_collections=end_points_collection):
net = slim.repeat(inputs, 2, slim.conv2d, 64, [3, 3], scope='conv1')
net = slim.max_pool2d(net, [2, 2], scope='pool1')
net = slim.repeat(net, 2, slim.conv2d, 128, [3, 3], scope='conv2')
net = slim.max_pool2d(net, [2, 2], scope='pool2')
net = slim.repeat(net, 3, slim.conv2d, 256, [3, 3], scope='conv3')
net = slim.max_pool2d(net, [2, 2], scope='pool3')
net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='conv4')
net = slim.max_pool2d(net, [2, 2], scope='pool4')
net = slim.repeat(net, 3, slim.conv2d, 512, [3, 3], scope='conv5')
net = slim.max_pool2d(net, [2, 2], scope='pool5')
# Use conv2d instead of fully_connected layers.
net = slim.conv2d(net, 4096, [7, 7], padding=fc_conv_padding, scope='fc6')
net = slim.dropout(net, dropout_keep_prob, is_training=is_training,
scope='dropout6')
net = slim.conv2d(net, 4096, [1, 1], scope='fc7')
# Convert end_points_collection into a end_point dict.
end_points = slim.utils.convert_collection_to_dict(end_points_collection)
if global_pool:
net = tf.reduce_mean(net, [1, 2], keep_dims=True, name='global_pool')
end_points['global_pool'] = net
if num_classes:
net = slim.dropout(net, dropout_keep_prob, is_training=is_training,
scope='dropout7')
net = slim.conv2d(net, num_classes, [1, 1],
activation_fn=None,
normalizer_fn=None,
scope='fc8')
if spatial_squeeze:
net = tf.squeeze(net, [1, 2], name='fc8/squeezed')
end_points[sc.name + '/fc8'] = net
return net, end_points
vgg_16.default_image_size = 224
def vgg_19(inputs,
num_classes=1000,
is_training=True,
dropout_keep_prob=0.5,
spatial_squeeze=True,
scope='vgg_19',
fc_conv_padding='VALID',
global_pool=False):
with tf.variable_scope(scope, 'vgg_19', [inputs]) as sc:
end_points_collection = sc.original_name_scope + '_end_points'
# Collect outputs for conv2d, fully_connected and max_pool2d.
with slim.arg_scope([slim.conv2d, slim.fully_connected, slim.max_pool2d],
outputs_collections=end_points_collection):
net = slim.repeat(inputs, 2, slim.conv2d, 64, [3, 3], scope='conv1')
net = slim.max_pool2d(net, [2, 2], scope='pool1')
net = slim.repeat(net, 2, slim.conv2d, 128, [3, 3], scope='conv2')
net = slim.max_pool2d(net, [2, 2], scope='pool2')
net = slim.repeat(net, 4, slim.conv2d, 256, [3, 3], scope='conv3')
net = slim.max_pool2d(net, [2, 2], scope='pool3')
net = slim.repeat(net, 4, slim.conv2d, 512, [3, 3], scope='conv4')
net = slim.max_pool2d(net, [2, 2], scope='pool4')
net = slim.repeat(net, 4, slim.conv2d, 512, [3, 3], scope='conv5')
net = slim.max_pool2d(net, [2, 2], scope='pool5')
# Use conv2d instead of fully_connected layers.
net = slim.conv2d(net, 4096, [7, 7], padding=fc_conv_padding, scope='fc6')
net = slim.dropout(net, dropout_keep_prob, is_training=is_training,
scope='dropout6')
net = slim.conv2d(net, 4096, [1, 1], scope='fc7')
# Convert end_points_collection into a end_point dict.
end_points = slim.utils.convert_collection_to_dict(end_points_collection)
if global_pool:
net = tf.reduce_mean(net, [1, 2], keep_dims=True, name='global_pool')
end_points['global_pool'] = net
if num_classes:
net = slim.dropout(net, dropout_keep_prob, is_training=is_training,
scope='dropout7')
net = slim.conv2d(net, num_classes, [1, 1],
activation_fn=None,
normalizer_fn=None,
scope='fc8')
if spatial_squeeze:
net = tf.squeeze(net, [1, 2], name='fc8/squeezed')
end_points[sc.name + '/fc8'] = net
return net, end_points
vgg_19.default_image_size = 224
# Alias
vgg_d = vgg_16
vgg_e = vgg_19
8. 模型参数计算

Network in Network
1. background
1.1 CNN 提取局部图像特征的方式及不足
CNN 通过与不同大小的卷积核做卷积操作来提取不同视野范围的局部图片块(local patches)的特征,再将结果通过激活函数(rectifier、sigmoid、tanh等)输出,再做 Pooling。
CNN 由卷积层与池化层交替组成,卷积层通过使用非线性激活函数(ReLU、sigmoid、tanh等)的线性组合形成 feature map。实际上 CNN 中的卷积操作(也可看做两个向量的内积)是一种广义线性模型。如果所要提取的特征是线性的或者低度非线性的,这种卷积操作得到的特征是比较符合预期的,但是如果所要提取的特征是高度非线性的,用 CNN 中的 filter 方法想要获取到符合我们预期的特征就比较困难了,这个时候传统 CNN 会尝试使用超完备的滤波器来提取各种潜在的特征,即初始化大量的滤波器提取尽可能多的特征,将我们期望的特征也覆盖到,这样导致的一个结果就是:网络结果复杂,参数空间巨大。
1.2 目的
提高模型对感受野中的局部区域的分辨能力,从而使得网络的分类效果更好。
1.3 传统方法存在的问题
- 当潜在概念的实例是线性可分的时候,线性卷积核有足够提取抽象特征的能力。但是,要想得到更好的抽象特征,通常需要依靠非线性函数。
- 在传统的卷积神经网络中,全连接层是一个黑匣子,很难知道反向传播的具体情况。但是全局平均池化层(本文设计的一个结构)更有意义且解释性更高。另外,全连接层更易过拟合且依赖正则化操作,但是全局平均池化层本身就有正则化的意义。
1.4 解决问题的方法
针对问题 1,作者认为设计一个更加通用的函数逼近器(即不管数据是否是线性可分的)来对局部块进行特征提取是极为重要的,其中最为通用的函数逼近器有两个:径向基函数网络和多层感知机。作者选择了多层感知机作为传统卷积核的替代,理由有两点:
- 与 CNN 兼容,可以用反向传播训练
- 多层感知机本身是一个很深的模型,与特征重用的理念相符合。
针对问题 2,采用全局平均池化层来取代传统的全连接层。两者的主要区别在于变换矩阵。全连接层有一个密集的变换矩阵,值容易受反向传播的影响,以至于容易过拟合。但是对比来看,全局平均池化层不易受到反向传播优化的影响,可以看看下面全局平均池化层的具体操作。作者在 CIFAR-10 上做了对比实验:

2. NIN 中的改进点(创新点)
2.1 MPL-conv
Network in Network 中用一个更强的非线性函数逼近器来提升 local patches 的抽象能力。这种非线性逼近器可以有多种选择,作者使用了多层感知机(perceptron)作为 micro network,也就是非线性逼近结构,这种 micro network 也称为 MLP。MLP 卷积层可以看成是在传统 CNN 卷积层中再包含一个微型的多层网络(如下图所示)。事实上,CNN 高层特征其实是底层特征通过某种运算的组合,通过利用多层 MLP 的微型网络,可以对局部视野下的神经元进行更加复杂的运算,提高非线性。
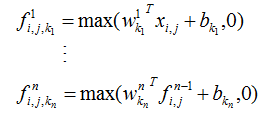
选择多层感知机 MLP 作为 micro network 主要基于两个目的:
- MLP 的参数可以使用 BP 算法训练,与 CNN 高度整合。
- MLP 可自行深度化(可以增加 hidden layer),符合特征复用的思想。

从上图可以看出改进的多层感知机构成的卷积层和传统的卷积层的差别,MLP-conv layer 有更好的非线性能力,可以提取更加抽象的特征,具体卷积步骤和传统的线性卷积核一样。MLP-conv layer 也被称作 micro neural network,多个 MLP-conv layer 进行堆叠,构成了整个特征提取层。
MLP 在 CNN 基础上的进步在于:
将 feature map 由多通道的线性组合变为非线性组合,提高特征抽象能力。
通过
1x1卷积核及 global avg-pooling 代替 fully connected layers 实现减小参数。
事实上,CNN 里的卷积基本上是多通道的 feature map 和多通道的卷积核做操作,如果使用 1x1 的卷积核,得到的值就与周边的像素点无关了,则这个操作实现的就是多个 feature map 的线性组合,实现 feature map 在通道个数上的变化。多个 1x1 的卷积核级联就可以实现对多通道的 feature map 做非线性的组合,再配合激活函数,就可以实现 MLP 结构,同时通过 1x1 的卷积核操作还可以实现卷积核通道数的降维和升维,实现参数的减小化。
通过 MLP 微结构,实现了不同 filter 得到的不同 feature map 之间的整合,可以使网络学习到复杂和有用的跨特征图特征。MLP 中的每一层相当于一个卷积核为 1x1 的卷积层。
2.2 Global Average Pooling
对于分类问题,最后一个卷积层的 feature map 通常与全连接层连接,最后通过 softmax 逻辑回归分类。全连接层带来的问题就是参数空间过大,容易过拟合。早期 Alex 采用了Dropout 的方法,来减轻过拟合,提高网络的泛化能力,但依旧无法解决参数过多问题。
利用全局均值池化来替代原来的全连接层(fully connected layers),即对每个特征图一整张图片进行全局均值池化,则每张特征图得到一个输出。例如 CIFAR-100 分类任务,直接将最后一层 MLPconv 输出通道设为 100,对每个 feature map(共 100 个)进行平局池化得到 100 维的输出向量,对应 100 种图像分类。这样采用均值池化,去除了构建全连接层的大量参数,大大减小网络规模,有效避免过拟合。
全连接层比较容易过拟合,影响整个模型的泛化能力,dropout 的引入部分解决了 dense layer 的过拟合问题。global average pooling 的优势在于只是平均,没有参数。其使用了卷积层 + dense layer,很难解释从 loss back-propagate 回去的是什么,更像是一个黑盒子,而 global average 用简单的 average 建立起了 feature map 和 category 之间的联系,简单来说,以手写体识别的分类问题为例,就是每个类别仅仅对应一个 feature map,每个 feature map 内部求平均,10 个 feature map 就变成了一个 10 维向量,然后输入到 softmax 中。全连接层过于依赖 dropout 来避免过拟合,而 global average pooling 可以看做是一种结构化正则,即对多个 feature map 的空间平均(spatial average),能够应对输入的许多空间变化(翻转、平移等)。
注意,global average pooling 与 (local) average pooling 之间的区别。对于 10个 6*6 的 feature map,global average pooling的输出是 10*1 维的向量,average pooling 的输出则是根据 pool_size,strides,padding 计算出来的 10 个 feature map。某种程度上说,global average pooling 只是 average pooling 的一个特例。
因此使用全局平均 pooling 代替全连接层,使得最后一个多层感知卷积层获得的每一个特征图能够对应于一个输出类别,优点如下:
- 全局平均池化更原生的支持于卷积结构,通过加强特征映射与相应分(种)类的对应关系,特征映射可以很容易地解释为分类映射。
- 全局平均池化一层没有需要优化的参数,减少大量的训练参数有效避免过拟合。
- 全局平均池化汇总(求和)空间信息,因此其对空间变换是健壮的。
最后,总结下 NIN 的主要优点:
- 更好的局部抽象能力
- 更小的参数空间
- 更小的全局 over-fitting
Inception v1(GoogLeNet)
源自论文 《Going Deeper with Convolutions》
2014 年,GoogLeNet 和 VGG 是当年 ImageNet 挑战赛(ILSVRC14)的双雄,GoogLeNet 获得了第一名、VGG 获得了第二名,这两类模型结构的共同特点是层次更深了。
VGG 继承了 LeNet 以及 AlexNet 的一些框架结构,而 GoogLeNet 则做了更加大胆的网络结构尝试,虽然深度只有
22层,但大小却比 AlexNet 和 VGG 小很多,GoogleNet 参数为500万个,AlexNet 参数个数是 GoogleNet 的12倍,VGG 参数又是 AlexNet 的3倍,因此在内存或计算资源有限时,GoogleNet 是比较好的选择;从模型结果来看,GoogLeNet 的性能却更加优越。不过 VGG 相对延续传统的结构也给它带来了优势,便于理解,泛化到其他类型的任务时效果也非常的好。
1. 简介
GoogLeNet 的参数量相比 AlexNet 要少很多,是 AlexNet 参数的
1/12(12xfewer parameters than AlexNet)由于手机终端和嵌入式设备的发展,深度学习算法的运行效率和内存控制显得尤其重要,深度神经网络不仅具有学术性,更应该能够应用于现实生活中
论文起源于 NIN(Network in Network),并且在网络深度上进行了研究
2. 研究动机
针对之前的网络结构设计,主要存在几个方面的缺点:
参数太多,模型的熵容量太大,容易导致过拟合,尤其对于比较小的数据集
网络越大,计算复杂度也就越大,在实际应用中,带来了困难
网络越深,模型训练越困难,梯度消失问题不可避免
GoogLeNet 的研究动机从两个方面进行考虑:
深度: 网络采用了一个
22层的结构,9个 Inception(2-5-2结构),但是为了避免梯度消失问题,GoogLeNet 在不同层增加了 Loss 的输出宽度: 网络在每一个小的结构中,利用了
1x1,3x3,5x5的卷积核和直接 Max Pooling 操作(为了保证输出的特征层的大小与卷积核输出大小相同,步长设置为1),为了避免由于宽度的增加带来每一个卷机核或者 Max Pooling 输出的特征层 cancate 之后,特征层的深度过深,也为了减少网络参数,在每一个3x3,5x5的卷积核前面和3x3Max Pooling 后面都利用了一个1x1的卷积核进行降维,如下图:

3. 网络结构
网络结构中的具体参数:

说明:
- 前面
4层,为普通的卷积和 max pooling 操作。在网络的开始利用了7x7,s=2的 filter,其目的是为了降低图像的特征层大小,减少后面的计算量 - 结构中的 Max Pooling 采用的类似于 AlexNet 中的 Overlapping Pooling (
3x3,s=2) - 网络中,不断重复上述的 Inception Module 模块,来提高网络的深度:
#1x1:表示网络结构中的最左边的1x1卷积核个数#3x3reduce: 表示网络结构进行3x3卷积操作之前1x1卷积核的个数#3x3: 表示网络结构中的3x3卷积核个数#5x5reduce: 表示网络结构进行5x5卷积操作之前1x1卷积核的个数#5x5: 表示网络结构中的5x5卷积核个数pool proj:表示进行3x3max pooling 操作之后,1x1卷积核的个数
- 所有的网络中的操作,后面都接一个非线性映射变换 ReLU
- 网络的最后,采用了类似 NIN 网络结构中的 global pooling 操作,对
7x7x1024的特征层进行 avg pooling 操作,变成了一个1x1x1024的向量 - 采用 dropout 操作,避免过拟合
网络的深度增加,给训练带来了很大的困难(梯度消失问题),为了更好的训练网络,GoogLeNet 在 Inception(4a)和 Inception(4d)的输出层,增了 Loss 计算误差,然后反向传播,在整个训练过程中,不断减少这个两个 Loss 的权重。

4. 核心思想
Inception 模块的基本机构如下图,整个 Inception 结构就是由多个这样的 Inception 模块串联起来的。Inception 结构的主要贡献有两个:
- 使用
1x1的卷积来进行升降维 - 在多个尺寸上同时进行卷积再聚合

4.1 1x1 的卷积
可以看到上图中有多个黄色的 1x1 卷积模块,这样的卷积有什么用处呢?
作用 1:在相同尺寸的感受野中叠加更多的卷积,能提取到更丰富的特征。这个观点来自于 《Network in Network》(NIN),上图里三个 1x1 卷积都起到了该作用。

上图左侧是是传统的卷积层结构(线性卷积),在一个尺度上只有一次卷积;右图是 Network in Network 结构(NIN结构),先进行一次普通的卷积(比如 3x3),紧跟再进行一次 1x1 的卷积,对于某个像素点来说,1x1 卷积等效于该像素点在所有特征上进行一次全连接的计算,所以右侧图的 1x1 卷积画成了全连接层的形式【需要注意的是:NIN 结构中,无论是第一个 3x3 卷积还是新增的 1x1 卷积,后面都紧跟着激活函数(比如 ReLU)】。
将两个卷积串联,就能组合出更多的非线性特征。举个例子,假设第 1 个 3x3 卷积+激活函数近似于: ,第二个
,第二个 1x1 卷积+激活函数近似于: ,那
,那 和
和 比,哪个非线性更强,更能模拟非线性的特征?答案是显而易见的。NIN 的结构和传统的神经网络中多层的结构有些类似,后者的多层是跨越了不同尺寸的感受野(通过层与层中间加 pooling 层),从而在更高尺度上提取出特征;NIN 结构是在同一个尺度上的多层(中间没有pool层),从而在相同的感受野范围能提取更强的非线性。
比,哪个非线性更强,更能模拟非线性的特征?答案是显而易见的。NIN 的结构和传统的神经网络中多层的结构有些类似,后者的多层是跨越了不同尺寸的感受野(通过层与层中间加 pooling 层),从而在更高尺度上提取出特征;NIN 结构是在同一个尺度上的多层(中间没有pool层),从而在相同的感受野范围能提取更强的非线性。
作用 2:使用 1x1 卷积进行降维,降低了计算复杂度。上图中间 3x3 卷积和 5x5 卷积前的 1x1 卷积都起到了这个作用。当某个卷积层输入的特征数较多,对这个输入进行卷积运算将产生巨大的计算量;如果对输入先进行降维,减少特征数后再做卷积计算量就会显著减少。
下图是优化前后两种方案的乘法次数比较,同样是输入一组有 192 个特征、32x32 大小,输出 256 组特征的数据。第一张图直接用 3x3 卷积实现,需要 192x256x3x3x32x32=452984832 次乘法;第二张图先用 1x1 的卷积降到 96 个特征(则卷积核为:1x1x96),再用 3x3 卷积恢复出256组特征,需要 192x96x1x1x32x32+96x256x3x3x32x32=245366784 次乘法,使用 1x1 卷积降维的方法节省了一半的计算量(注意:因为卷积核深度为 96,而输入层的通道数为 192,由于卷积核中的通道数量必须和输入层中的通道数量保持一致,所以最终的通道数为96,便实现了通道数量的压缩)。

有人会问,用 1x1 卷积降到 96 个特征后特征数不就减少了么,会影响最后训练的效果么?答案是否定的,只要最后输出的特征数不变(256 组),中间的降维类似于压缩的效果,并不影响最终训练的结果。
4.2 多个尺寸上进行卷积再聚合

从上图可以看到对输入做了 4 个分支,分别用不同尺寸的 filter 进行卷积或池化,最后再在特征维度上拼接到一起。这种全新的结构有什么好处呢?Szegedy 从多个角度进行了解释:
解释 1:从直观感觉上在多个尺度上同时进行卷积,能提取到不同尺度的特征。特征更为丰富也意味着最后分类判断时更加准确。
解释 2:利用稀疏矩阵分解成密集矩阵计算的原理来加快收敛速度。举个例子下图左侧是个稀疏矩阵(很多元素都为
0,不均匀分布在矩阵中),和一个2x2的矩阵进行卷积,需要对稀疏矩阵中的每一个元素进行计算;如果像右图那样把稀疏矩阵分解成2个子密集矩阵,再和2x2矩阵进行卷积,稀疏矩阵中0较多的区域就可以不用计算,计算量就大大降低。这个原理应用到 Inception 上就是要在特征维度上进行分解!传统的卷积层的输入数据只和一种尺度(比如3x3)的卷积核进行卷积,输出固定维度(比如256个特征)的数据,所有256个输出特征基本上是均匀分布在3x3尺度范围上,这可以理解成输出了一个稀疏分布的特征集;而 Inception 模块在多个尺度上提取特征(比如1x1,3x3,5x5),输出的256个特征就不再是均匀分布,而是相关性强的特征聚集在一起(比如1x1的的96个特征聚集在一起,3x3的96个特征聚集在一起,5x5的64个特征聚集在一起),这可以理解成多个密集分布的子特征集。这样的特征集中因为相关性较强的特征聚集在了一起,不相关的非关键特征就被弱化,同样是输出256个特征,Inception 方法输出的特征“冗余”的信息较少。用这样的“纯”的特征集层层传递最后作为反向计算的输入,自然收敛的速度更快。
解释 3:Hebbin 赫布原理。Hebbian 原理是神经科学上的一个理论,解释了在学习的过程中脑中的神经元所发生的变化,用一句话概括就是:fire together, wire together。赫布认为“两个神经元或者神经元系统,如果总是同时兴奋,就会形成一种‘组合’,其中一个神经元的兴奋会促进另一个的兴奋”。比如狗看到肉会流口水,反复刺激后,脑中识别肉的神经元会和掌管唾液分泌的神经元会相互促进,“缠绕”在一起,以后再看到肉就会更快流出口水。用在 Inception 结构中就是要把相关性强的特征汇聚到一起。这有点类似上面的解释 2,把
1x1,3x3,5x5的特征分开。因为训练收敛的最终目的就是要提取出独立的特征,所以预先把相关性强的特征汇聚,就能起到加速收敛的作用。在 Inception 模块中有一个分支使用了 max pooling,作者认为 pooling 也能起到提取特征的作用,所以也加入模块中。注意这个 pooling的stride=1,pooling 后没有减少数据的尺寸。
5. 论文关键点解析
Page 3:The fundamental way of solving both issues would be by ultimately moving from fully connected to sparsely connected architectures, even inside the convolutions. Besides mimicking biological systems, this would also have the advantage of firmer theoretical underpinnings due to the ground-breaking work of Arora et al. [2]. Their main result states that if the probability distribution of the data-set is representable by a large, very sparse deep neural network, then the optimal network topology can be constructed layer by layer by analyzing the correlation statistics of the activations of the last layer and clustering neurons with highly correlated outputs.
作者提出需要将全连接的结构转化成稀疏连接的结构。稀疏连接有两种方法:一种是空间(spatial)上的稀疏连接,也就是传统的 CNN 卷积结构:只对输入图像的某一部分 patch 进行卷积,而不是对整个图像进行卷积,共享参数降低了总参数的数目减少了计算量;另一种方法是在特征(feature)维度进行稀疏连接,就是前一节提到的在多个尺寸上进行卷积再聚合,把相关性强的特征聚集到一起,每一种尺寸的卷积只输出 256 个特征中的一部分,这也是种稀疏连接。作者提到这种方法的理论基础来自于论文 《Provable bounds for learning some deep representations》。
Page 3:On the downside, todays computing infrastructures are very inefficient when it comes to numerical calculation on non-uniform sparse data structures. Even if the number of arithmetic operations is reduced by100×, the overhead of lookups and cache misses is so dominant that switching to sparse matrices would not pay off. The gap is widened even further by the use of steadily improving, highly tuned, numerical libraries that allow for extremely fast dense matrix multiplication, exploit-ing the minute details of the underlying CPU or GPU hardware [16,9]. Also, non-uniform sparse models require more sophisticated engineering and computing infrastructure. Most current vision oriented machine learning systems utilize sparsity in the spatial domain just by the virtue of employing convolutions. However, convolutions are implemented as collections of dense connections to the patches in the earlier layer. ConvNets have traditionally used random and sparse connection tables in the feature dimensions since [11] in order to break the symmetry and improve learning, the trend changed back to full connections with [9] in order to better optimize parallel computing. The uniformity of the structure and a large number of filters and greater batch size allow for utilizing efficient dense computation.
作者提到如今的计算机对稀疏数据进行计算的效率是很低的,即使使用稀疏矩阵算法也得不偿失(之前将稀疏矩阵分解成子密集矩阵来进行计算的方法,注意图中左侧的那种稀疏矩阵在计算机内部都是使用元素值+行列值的形式来存储,只存储非 0 元素)。使用稀疏矩阵算法来进行计算虽然计算量会大大减少,但会增加中间缓存(具体原因请研究稀疏矩阵的计算方法)。
当今最常见的利用数据稀疏性的方法是通过卷积对局部 patch 进行计算(CNN 方法,就是前面提到的在 spatial 上利用稀疏性);另一种利用数据稀疏性的方法是在特征维度进行利用,比如ConvNets 结构,它使用特征连接表来决定哪些卷积的输出才累加到一起(普通结构使用一个卷积核对所有输入特征做卷积,再将所有结果累加到一起,输出一个特征; 而 ConvNets 是选择性的对某些卷积结果做累加)。ConvNets 利用稀疏性的方法现在已经很少用了,因为只有在特征维度上进行全连接才能更高效的利用 GPU 的并行计算的能力,否则你就得为这样的特征连接表单独设计 CUDA 的接口函数,单独设计的函数往往无法最大限度的发挥 GPU 并行计算的能力。
Page 3:This raises the question whether there is any hope for a next, intermediate step: an architecture that makes use of the extra sparsity, even at filter level, as suggested by the theory, but exploits our current hardware by utilizing computations on dense matrices. The vast literature on sparse matrix computations (e.g. [3]) suggests that clustering sparse matrices into relatively dense submatrices tends to give state of the art practical performance for sparse matrix multiplication.
前面提到 ConvNets 这样利用稀疏性的方法现在已经很少用了,那还有什么方法能在特征维度上利用稀疏性么?这就引申出了这篇论文的重点:将相关性强的特征汇聚到一起,也就是之前提到的在多个尺度上卷积再聚合。
page 4:In order to avoid patch-alignment issues, current incarnations of the Inception architecture are restricted to filter sizes 1×1,3×3 and 5×5, however this decision was based more on convenience rather than necessity. It also means that the suggested architecture is a combination of all those layers with their output filter
banks concatenated into a single output vector forming the input of the next stage. Additionally, since pooling operations have been essential for the success in current state of the art convolutional networks, it suggests that adding an alternative parallel pooling path in each such stage should have additional beneficial effect, too (see Figure 2(a))
论文这几句解释了最基本的“ Inception module”的构成:

所以在一层里把不同大小的卷积核叠在一起后,意味着一层里可以产生不同大小的卷积核处理之后的效果,也意味着不用人为的来选择这一层要怎么卷,这个网络自己便会学习用什么样的卷积(或池化)操作最好。

但是作者发现由于通道数量太多了,这样计算成本会变得非常高(第三段),所以 1×1 卷积再次登场,用来压缩通道数量,缩减了计算成本(第四段/下边这段)。
This leads to the second idea of the proposed architecture: judiciously applying dimension reductions and projections wherever the computational requirements would increase too much otherwise.This is based on the success of embeddings: even low dimensional embeddings might contain a lot of information about a relatively large image patch. However, embeddings represent information in a dense, compressed form and compressed information is harder to model. We would like to keep our representation sparse at most places (as required by the conditions of [2]) and compress the signals only whenever they have to be aggregated en masse. That is, 1×1 convolutions are used to compute reductions before the expensive 3×3 and 5×5 convolutions. Besides being used as reductions, they also include the use of rectified linear activation which makes them dual-purpose. The final result is depicted in Figure 2(b).
即先用 1×1 卷积压缩通道数量,再让3×3,5×5 来进行滤波:

最终“Inception module”变成了下边的样子:

Page 6:The use of average pooling before the classifier is based on [12], although our implementation differs in that we use an extra linear layer.
Network in Network(NIN)最早提出了用 Global Average Pooling(GAP)层来代替全连接层的方法,具体方法就是:对每一个 feature 上的所有点做平均,有 n 个 feature 就输出 n 个平均值作为最后的 softmax 的输入。它的好处:
- 对数据在整个 feature 上作正则化,防止了过拟合
- 不再需要全连接层,减少了整个结构参数的数目(一般全连接层是整个结构中参数最多的层),过拟合的可能性降低
- 不用再关注输入图像的尺寸,因为不管是怎样的输入都是一样的平均方法,传统的全连接层要根据尺寸来选择参数数目,不具有通用性。
Page 6:By adding auxiliary classifiers connected to these intermediate layers, we would expect to encourage discrimination in the lower stages in the classifier, increase the gradient signal that gets propagated back, and provide additional regularization.
Inception 结构在在某些层级上加了分支分类器,输出的 loss 乘以个系数再加到总的 loss 上,作者认为可以防止梯度消失问题(事实上在较低的层级上这样处理基本没作用,作者在后来的 inception v3 论文中做了澄清)。
6. 论文的亮点

1x1 卷积的好处:

1x1 卷积主要在做这些事:


如果用 1x1 卷积去处理 6x6x32 的图,相当于给这 32 个通道的同一个位置分配相同的权重。如果用 1x1x32 的卷积去处理 6x6x32 的图,则可以给 32 个通道分配不同的权重。
1x1 卷积还可以压缩通道数量:

1x1 卷积相对于其他的滤波器组参数几何倍数减少,毕竟 1x1卷积只有一个参数,3x3 有 9 个参数,5x5 有 25个……..
7. GoogLeNet slim 实现
import tensorflow as tf
slim = tf.contrib.slim
trunc_normal = lambda stddev: tf.truncated_normal_initializer(0.0, stddev)
def inception_arg_scope(weight_decay=0.00004,
use_batch_norm=True,
batch_norm_decay=0.9997,
batch_norm_epsilon=0.001,
activation_fn=tf.nn.relu,
batch_norm_updates_collections=tf.GraphKeys.UPDATE_OPS,
batch_norm_scale=False):
'''
Args:
weight_decay: The weight decay to use for regularizing the model.
use_batch_norm: "If `True`, batch_norm is applied after each convolution.
batch_norm_decay: Decay for batch norm moving average.
batch_norm_epsilon: Small float added to variance to avoid dividing by zero
in batch norm.
activation_fn: Activation function for conv2d.
batch_norm_updates_collections: Collection for the update ops for
batch norm.
batch_norm_scale: If True, uses an explicit `gamma` multiplier to scale the
activations in the batch normalization layer.
Returns:
An `arg_scope` to use for the inception models.
'''
batch_norm_params = {
# Decay for the moving averages.
'decay': batch_norm_decay,
# epsilon to prevent 0s in variance.
'epsilon': batch_norm_epsilon,
# collection containing update_ops.
'updates_collections': batch_norm_updates_collections,
# use fused batch norm if possible.
'fused': None,
'scale': batch_norm_scale,
}
if use_batch_norm:
normalizer_fn = slim.batch_norm
normalizer_params = batch_norm_params
else:
normalizer_fn = None
normalizer_params = {}
# Set weight_decay for weights in Conv and FC layers.
with slim.arg_scope([slim.conv2d, slim.fully_connected],
weights_regularizer=slim.l2_regularizer(weight_decay)):
with slim.arg_scope(
[slim.conv2d],
weights_initializer=slim.variance_scaling_initializer(),
activation_fn=activation_fn,
normalizer_fn=normalizer_fn,
normalizer_params=normalizer_params) as sc:
return sc
def inception_v1_base(inputs,
final_endpoint='Mixed_5c',
scope='InceptionV1'):
'''
Args:
final_endpoint: specifies the endpoint to construct the network up to. It
can be one of ['Conv2d_1a_7x7', 'MaxPool_2a_3x3', 'Conv2d_2b_1x1',
'Conv2d_2c_3x3', 'MaxPool_3a_3x3', 'Mixed_3b', 'Mixed_3c',
'MaxPool_4a_3x3', 'Mixed_4b', 'Mixed_4c', 'Mixed_4d', 'Mixed_4e',
'Mixed_4f', 'MaxPool_5a_2x2', 'Mixed_5b', 'Mixed_5c']
Returns:
A dictionary from components of the network to the corresponding activation.
'''
end_points = {}
with tf.variable_scope(scope, 'Inception_v1', [inputs]):
with slim.arg_scope([slim.conv2d, slim.fully_connected],
weights_initializer=trusnc_normal(0.01)):
with slim.arg_scope([slim.conv2d, slim.max_pool2d],
stride=1, padding='SAME'):
end_point = 'Conv2d_1a_7x7'
net = slim.conv2d(inputs, 64, [7,7], stride=2, scope=end_point)
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'MaxPool_2a_3x3'
net = slim.max_pool2d(net, [3,3], stride=2, scope=end_point)
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Conv2d_2b_1x1'
net = slim.conv2d(net, 64, [1,1], scope=end_point)
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Conv2d_2c_3x3'
net = slim.conv2d(net, 192, [3,3], scope=end_point)
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'MaxPool_3a_3x3'
net = slim.max_pool2d(net, [3,3], stride=2, scope=end_point)
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Mixed_3b'
with tf.variable_scope(end_point):
with tf.variable_scope('Branch_0'):
branch_0 = slim.conv2d(net, 64, [1,1], scope='Conv2d_0a_1x1')
with tf.variable_scope('Branch_1'):
branch_1_1 = slim.conv2d(net, 96, [1,1], scope='Conv2d_0a_1x1')
branch_1_2 = slim.conv2d(branch_1_1, 128, [3,3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_2'):
branch_2_1 = slim.conv2d(net, 16, [1,1], scope='Conv2d_0a_1x1')
branch_2_2 = slim.conv2d(branch_2_1, 32, [3,3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_3'):
branch_3_1 = slim.max_pool2d(net, [3,3], scope='MaxPool_0a_3x3')
branch_3_2 = slim.conv2d(branch_3_1, 32, [1,1], scope='Conv2d_0b_1x1')
net = tf.concat(axis=3,
values=[branch_0, branch_1_2, branch_2_2, branch_3_2])
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Mixed_3c'
with tf.variable_scope(end_point):
with tf.variable_scope('Branch_0'):
branch_0 = slim.conv2d(net, 128, [1,1], scope='Conv2d_0a_1x1')
with tf.variable_scope('Branch_1'):
branch_1_1 = slim.conv2d(net, 128, [1,1], scope='Conv2d_0a_1x1')
branch_1_2 = slim.conv2d(branch_1_1, 192, [3,3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_2'):
branch_2_1 = slim.conv2d(net, 32, [1, 1], scope='Conv2d_0a_1x1')
branch_2_2 = slim.conv2d(branch_2_1, 96, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_3'):
branch_3_1 = slim.max_pool2d(net, [3, 3], scope='MaxPool_0a_3x3')
branch_3_2 = slim.conv2d(branch_3_1, 64, [1, 1], scope='Conv2d_0b_1x1')
net = tf.concat(axis=3,
values=[branch_0, branch_1_2, branch_2_2, branch_3_2])
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'MaxPool_4a_3x3'
net = slim.max_pool2d(net, [3, 3], stride=2, scope=end_point)
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Mixed_4b'
with tf.variable_scope(end_point):
with tf.variable_scope('Branch_0'):
branch_0 = slim.conv2d(net, 192, [1, 1], scope='Conv2d_0a_1x1')
with tf.variable_scope('Branch_1'):
branch_1_1 = slim.conv2d(net, 96, [1, 1], scope='Conv2d_0a_1x1')
branch_1_2 = slim.conv2d(branch_1_1, 208, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_2'):
branch_2_1 = slim.conv2d(net, 16, [1, 1], scope='Conv2d_0a_1x1')
branch_2_2 = slim.conv2d(branch_2_1, 48, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_3'):
branch_3_1 = slim.max_pool2d(net, [3, 3], scope='MaxPool_0a_3x3')
branch_3_2 = slim.conv2d(branch_3_1, 64, [1, 1], scope='Conv2d_0b_1x1')
net = tf.concat(axis=3,
values=[branch_0, branch_1_2, branch_2_2, branch_3_2])
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Mixed_4c'
with tf.variable_scope(end_point):
with tf.variable_scope('Branch_0'):
branch_0 = slim.conv2d(net, 160, [1, 1], scope='Conv2d_0a_1x1')
with tf.variable_scope('Branch_1'):
branch_1_1 = slim.conv2d(net, 112, [1, 1], scope='Conv2d_0a_1x1')
branch_1_2 = slim.conv2d(branch_1_1, 224, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_2'):
branch_2_1 = slim.conv2d(net, 24, [1, 1], scope='Conv2d_0a_1x1')
branch_2_2 = slim.conv2d(branch_2_1, 64, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_3'):
branch_3_1 = slim.max_pool2d(net, [3, 3], scope='MaxPool_0a_3x3')
branch_3_2 = slim.conv2d(branch_3_1, 64, [1, 1], scope='Conv2d_0b_1x1')
net = tf.concat(axis=3,
values=[branch_0, branch_1_2, branch_2_2, branch_3_2])
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Mixed_4d'
with tf.variable_scope(end_point):
with tf.variable_scope('Branch_0'):
branch_0 = slim.conv2d(net, 128, [1, 1], scope='Conv2d_0a_1x1')
with tf.variable_scope('Branch_1'):
branch_1_1 = slim.conv2d(net, 128, [1, 1], scope='Conv2d_0a_1x1')
branch_1_2 = slim.conv2d(branch_1_1, 256, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_2'):
branch_2_1 = slim.conv2d(net, 24, [1, 1], scope='Conv2d_0a_1x1')
branch_2_2 = slim.conv2d(branch_2_1, 64, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_3'):
branch_3_1 = slim.max_pool2d(net, [3, 3], scope='MaxPool_0a_3x3')
branch_3_2 = slim.conv2d(branch_3_1, 64, [1, 1], scope='Conv2d_0b_1x1')
net = tf.concat(axis=3,
values=[branch_0, branch_1_2, branch_2_2, branch_3_2])
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Mixed_4e'
with tf.variable_scope(end_point):
with tf.variable_scope('Branch_0'):
branch_0 = slim.conv2d(net, 112, [1, 1], scope='Conv2d_0a_1x1')
with tf.variable_scope('Branch_1'):
branch_1_1 = slim.conv2d(net, 144, [1, 1], scope='Conv2d_0a_1x1')
branch_1_2 = slim.conv2d(branch_1_1, 288, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_2'):
branch_2_1 = slim.conv2d(net, 32, [1, 1], scope='Conv2d_0a_1x1')
branch_2_2 = slim.conv2d(branch_2_1, 64, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_3'):
branch_3_1 = slim.max_pool2d(net, [3, 3], scope='MaxPool_0a_3x3')
branch_3_2 = slim.conv2d(branch_3_1, 64, [1, 1], scope='Conv2d_0b_1x1')
net = tf.concat(axis=3,
values=[branch_0, branch_1_2, branch_2_2, branch_3_2])
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Mixed_4f'
with tf.variable_scope(end_point):
with tf.variable_scope('Branch_0'):
branch_0 = slim.conv2d(net, 256, [1, 1], scope='Conv2d_0a_1x1')
with tf.variable_scope('Branch_1'):
branch_1_1 = slim.conv2d(net, 160, [1, 1], scope='Conv2d_0a_1x1')
branch_1_2 = slim.conv2d(branch_1_1, 320, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_2'):
branch_2_1 = slim.conv2d(net, 32, [1, 1], scope='Conv2d_0a_1x1')
branch_2_2 = slim.conv2d(branch_2_1, 128, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_3'):
branch_3_1 = slim.max_pool2d(net, [3, 3], scope='MaxPool_0a_3x3')
branch_3_2 = slim.conv2d(branch_3_1, 128, [1, 1], scope='Conv2d_0b_1x1')
net = tf.concat(axis=3,
values=[branch_0, branch_1_2, branch_2_2, branch_3_2])
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'MaxPool_5a_2x2'
net = slim.max_pool2d(net, [2, 2], stride=2, scope=end_point)
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Mixed_5b'
with tf.variable_scope(end_point):
with tf.variable_scope('Branch_0'):
branch_0 = slim.conv2d(net, 256, [1, 1], scope='Conv2d_0a_1x1')
with tf.variable_scope('Branch_1'):
branch_1_1 = slim.conv2d(net, 160, [1, 1], scope='Conv2d_0a_1x1')
branch_1_2 = slim.conv2d(branch_1_1, 320, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_2'):
branch_2_1 = slim.conv2d(net, 32, [1, 1], scope='Conv2d_0a_1x1')
branch_2_2 = slim.conv2d(branch_2_1, 128, [3, 3], scope='Conv2d_0a_3x3')
with tf.variable_scope('Branch_3'):
branch_3_1 = slim.max_pool2d(net, [3, 3], scope='MaxPool_0a_3x3')
branch_3_2 = slim.conv2d(branch_3_1, 128, [1, 1], scope='Conv2d_0b_1x1')
net = tf.concat(axis=3,
values=[branch_0, branch_1_2, branch_2_2, branch_3_2])
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
end_point = 'Mixed_5c'
with tf.variable_scope(end_point):
with tf.variable_scope('Branch_0'):
branch_0 = slim.conv2d(net, 384, [1, 1], scope='Conv2d_0a_1x1')
with tf.variable_scope('Branch_1'):
branch_1_1 = slim.conv2d(net, 192, [1, 1], scope='Conv2d_0a_1x1')
branch_1_2 = slim.conv2d(branch_1_1, 384, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_2'):
branch_2_1 = slim.conv2d(net, 48, [1, 1], scope='Conv2d_0a_1x1')
branch_2_2 = slim.conv2d(branch_2_1, 128, [3, 3], scope='Conv2d_0b_3x3')
with tf.variable_scope('Branch_3'):
branch_3_1 = slim.max_pool2d(net, [3, 3], scope='MaxPool_0a_3x3')
branch_3_2 = slim.conv2d(branch_3_1, 128, [1, 1], scope='Conv2d_0b_1x1')
net = tf.concat(axis=3,
values=[branch_0, branch_1_2, branch_2_2, branch_3_2])
end_points[end_point] = net
if final_endpoint == end_point: return net, end_points
raise ValueError('Unknown final endpoint %s' % final_endpoint)
def inception_v1(inputs,
num_classes=1000,
is_training=True,
dropout_keep_prob=0.8,
prediction_fn=slim.softmax,
spatial_squeeze=True,
reuse=None,
scope='InceptionV1',
global_pool=False):
'''
Args:
inputs: a tensor of size [batch_size, height, width, channels].
num_classes: number of predicted classes. If 0 or None, the logits layer
is omitted and the input features to the logits layer (before dropout)
are returned instead.
is_training: whether is training or not.
dropout_keep_prob: the percentage of activation values that are retained.
prediction_fn: a function to get predictions out of logits.
spatial_squeeze: if True, logits is of shape [B, C], if false logits is of
shape [B, 1, 1, C], where B is batch_size and C is number of classes.
reuse: whether or not the network and its variables should be reused. To be
able to reuse 'scope' must be given.
scope: Optional variable_scope.
global_pool: Optional boolean flag to control the avgpooling before the
logits layer. If false or unset, pooling is done with a fixed window
that reduces default-sized inputs to 1x1, while larger inputs lead to
larger outputs. If true, any input size is pooled down to 1x1.
Returns:
net: a Tensor with the logits (pre-softmax activations) if num_classes
is a non-zero integer, or the non-dropped-out input to the logits layer
if num_classes is 0 or None.
end_points: a dictionary from components of the network to the corresponding
activation.
'''
# Final pooling and prediction
with tf.variable_scope(scope, 'InceptionV1', [inputs], reuse=reuse) as scope:
with slim.arg_scope([slim.batch_norm, slim.dropout],
is_training=is_training):
net, end_points = inception_v1_base(inputs, scope=scope)
with tf.variable_scope('Logits'):
if global_pool:
# Global average pooling.
net = tf.reduce_mean(net, [1, 2], keep_dims=True, name='global_pool')
end_points['global_pool'] = net
else:
# Pooling with a fixed kernel size.
net = slim.avg_pool2d(net, [7, 7], stride=1, scope='AvgPool_0a_7x7')
end_points['AvgPool_0a_7x7'] = net
if not num_classes:
return net, end_points
net = slim.dropout(net, dropout_keep_prob, scope='Dropout_0b')
logits = slim.conv2d(net, num_classes, [1, 1], activation_fn=None,
normalizer_fn=None, scope='Conv2d_0c_1x1')
if spatial_squeeze:
logits = tf.squeeze(logits, [1, 2], name='SpatialSqueeze')
end_points['Logits'] = logits
end_points['Predictions'] = prediction_fn(logits, scope='Predictions')
return logits, end_points
inception_v1.default_image_size = 224
inception_v1_arg_scope = inception_arg_scope
Inception v2(Batch Normalization)
源自 2015 年的论文 《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》
1. 提出背景
1.1 炼丹的困扰
在深度学习中,由于问题的复杂性,我们往往会使用较深层数的网络进行训练,但是对深层神经网络的训练调参更是困难且复杂。在这个过程中,需要去尝试不同的学习率、初始化参数方法(例如 Xavier 初始化)等方式来帮助模型加速收敛。深度神经网络之所以如此难训练,其中一个重要原因就是网络中层与层之间存在高度的关联性与耦合性。下图是一个多层的神经网络,层与层之间采用全连接的方式进行连接。

现规定左侧为神经网络的底层,右侧为神经网络的上层。那么网络中层与层之间的关联性会导致如下的状况:随着训练的进行,网络中的参数也随着梯度下降在不停更新。一方面,当底层网络中参数发生微弱变化时,由于每一层中的线性变换与非线性激活映射,这些微弱变化随着网络层数的加深而被放大(类似蝴蝶效应);另一方面,参数的变化导致每一层的输入分布会发生改变,进而上层的网络需要不停地去适应这些分布变化,使得模型训练变得困难。上述这一现象叫做 Internal Covariate Shift。
1.2 什么是 Internal Covariate Shift
Batch Normalization 的原论文作者给了 Internal Covariate Shift 一个较规范的定义:在深层网络训练的过程中,由于网络中参数变化而引起内部结点数据分布发生变化的这一过程被称作 Internal Covariate Shift。
这句话该怎么理解呢?以 1.1 中的图为例:
- 定义每一层的线性变换为:
 ,其中
,其中  代表层数
代表层数 - 非线性变换为:
 ,其中
,其中 为第
为第  层的激活函数
层的激活函数
随着梯度下降的进行,每一层的参数  和
和  都会被更新,那么
都会被更新,那么 的分布也就发生了改变,进而
的分布也就发生了改变,进而  也同样出现分布的改变。而
也同样出现分布的改变。而  作为第
作为第  层的输入,意味着
层的输入,意味着  层就需要去不停适应这种数据分布的变化,这一过程就被叫做 Internal Covariate Shift。
层就需要去不停适应这种数据分布的变化,这一过程就被叫做 Internal Covariate Shift。
1.3 Internal Covariate Shift 会带来什么问题?
(1)上层网络需要不停调整来适应输入数据分布的变化,导致网络学习速度的降低
在上面提到了梯度下降的过程会让每一层的参数 和
发生变化,进而使得每一层的线性与非线性计算结果分布产生变化。后层网络就要不停地去适应这种分布变化,这个时候就会使得整个网络的学习速率过慢。
(2)网络的训练过程容易陷入梯度饱和区,减缓网络收敛速度
当在神经网络中采用饱和激活函数(saturated activation function)时,例如 sigmoid,tanh 激活函数,很容易使得模型训练陷入梯度饱和区(saturated regime)。随着模型训练的进行,我们的参数 会逐渐更新并变大,此时
就会随之变大,并且
还受到更底层网络参数
的影响,随着网络层数的加深,
很容易陷入梯度饱和区,此时梯度会变得很小甚至接近于
0,参数的更新速度就会减慢,进而就会放慢网络的收敛速度。
对于激活函数梯度饱和问题,有两种解决思路。第一种就是更为非饱和性激活函数,例如 ReLU 可以在一定程度上解决训练进入梯度饱和区的问题。另一种思路是,可以让激活函数的输入分布保持在一个稳定状态来尽可能避免它们陷入梯度饱和区,这也就是 Normalization 的思路。
1.4 如何减缓 Internal Covariate Shift?
要缓解 ICS 问题,就要明白它产生的原因。ICS 产生的原因是由于参数更新带来的网络中每一层输入值分布的改变,并且随着网络层数的加深而变得更加严重,因此我们可以通过固定每一层网络输入值的分布来对减缓 ICS 问题。
(1)白化(Whitening)
白化(Whitening)是机器学习里面常用的一种规范化数据分布的方法,主要是 PCA 白化与 ZCA 白化。白化是对输入数据分布进行变换,进而达到以下两个目的:
- 使得输入特征分布具有相同的均值与方差。其中 PCA 白化保证了所有特征分布均值为
0,方差为1;而 ZCA 白化则保证了所有特征分布均值为0,方差相同。 - 去除特征之间的相关性。
通过白化操作,可以减缓 ICS 的问题,进而固定了每一层网络输入分布,加速网络训练过程的收敛。
(2)Batch Normalization提出
既然白化可以解决这个问题,为什么还要提出别的解决办法?当然是现有的方法具有一定的缺陷,白化主要有以下两个问题:
- 白化过程计算成本太高,并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作;
- 白化过程由于改变了网络每一层的分布,因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
既然有了上面两个问题,那我们的解决思路就很简单,一方面,提出的 Normalization 方法要能够简化计算过程;另一方面又需要经过规范化处理后让数据尽可能保留原始的表达能力。于是就有了简化+改进版的白化:Batch Normalization。
2. Batch Normalization
2.1 思路
既然白化计算过程比较复杂,那就简化一点,比如可以尝试单独对每个特征进行 Normalization 就可以了,让每个特征都有均值为 0,方差为 1 的分布就行。
另一个问题,既然白化操作减弱了网络中每一层输入数据表达能力,那就再加个线性变换操作,让这些数据再能够尽可能恢复本身的表达能力就好了。因此,基于上面两个解决问题的思路,作者提出了 Batch Normalization。
2.2 算法
在深度学习中,由于采用 full batch 的训练方式对内存要求较大,且每一轮训练时间过长;一般都会采用对数据做划分,用 mini-batch 对网络进行训练。因此,Batch Normalization 也就在 mini-batch 的基础上进行计算。
2.2.1 参数定义
依旧以下图这个神经网络为例,定义网络总共有 层(不包含输入层)并定义如下符号:

参数相关:
: 网络中的层标号
: 网络中的最后一层或总层数
: 第
层的维度,即神经元结点数
:第
层的权重矩阵,
: 第
层的偏置向量,
: 第
层的线性计算结果,
,
。
:第
层的激活函数
: 第
层的非线性激活结果,
样本相关:
:训练样本的数量
:训练样本的特征数
:训练样本集,
(注意这里
的一列是一个样本)
:batch size,即每个 batch 中样本的数量
:第
个 mini-batch 的训练数据,
,其中
2.2.2 算法步骤
介绍算法思路沿袭前面 BN 提出的思路来讲。第一点,对每个特征进行独立的 Normalization。考虑一个 batch 的训练,传入 m 个训练样本,并关注网络中的某一层,忽略上标 。
关注当前层的第 个维度,也就是第
个神经元结点,则有
。对当前维度进行规范化:
其中
是为了防止方差为
0产生无效计算。
结合个具体的例子来进行计算。下图只关注第 层的计算结果,左边的矩阵是
线性计算结果,还未进行激活函数的非线性变换。此时每一列是一个样本,图中可以看到共有
8 列,代表当前训练样本的 batch 中共有 8 个样本,每一行代表当前 层神经元的一个节点,可以看到当前
层共有
4 个神经元结点,即第 层维度为
4。可以看到,每行的数据分布都不同。

对于第一个神经元,可以求得 ,
(其中
),此时利用
对第一行数据(第一个维度)进行 Normalization 得到新的值
。同理可以计算出其他输入维度归一化后的值。如下图:

通过上面的变换,解决了第一个问题,即用更加简化的方式来对数据进行规范化,使得第 层的输入每个特征的分布均值为0,方差为
1。
如同上面提到的,Normalization 操作虽然缓解了 ICS 问题,让每一层网络的输入数据分布都变得稳定,但却导致了数据表达能力的缺失。也就是通过变换操作改变了原有数据的信息表达(representation ability of the network),使得底层网络学习到的参数信息丢失。另一方面,通过让每一层的输入分布均值为 0,方差为 1,会使得输入在经过 sigmoid 或 tanh 激活函数时,容易陷入非线性激活函数的线性区域。
因此,BN 又引入了两个可学习(learnable)的参数 与
。这两个参数的引入是为了恢复数据本身的表达能力,对规范化后的数据进行线性变换,即
。特别地,当
时,可以实现等价变换(identity transform)并且保留了原始输入特征的分布信息。
通过上面的步骤,我们就在一定程度上保证了输入数据的表达能力。
以上就是整个 Batch Normalization 在模型训练中的算法和思路。
补充: 在进行 normalization 的过程中,由于规范化操作会对减去均值,因此,偏置项
可以被忽略掉或可以被置为
0,即
2.2.3 公式
对于神经网络中的第 层,有:
3. 测试阶段如何使用 Batch Normalization?
BN 在每一层计算的 与
都是基于当前 batch 中的训练数据,但是这就带来了一个问题:在预测阶段,有可能只需要预测一个样本或很少的样本,没有像训练样本中那么多的数据,此时
与
的计算一定是有偏估计,这个时候该如何进行计算呢?
利用 BN 训练好模型后,保留了每组 mini-batch 训练数据在网络中每一层的 与
。此时使用整个样本的统计量来对测试数据(test data)进行归一化,具体来说使用均值与方差的无偏估计:
得到每个特征的均值与方差的无偏估计后,对测试数据采用同样的 normalization 方法:
另外,除了采用整体样本的无偏估计外。Ng 在 Coursera 上的 Deep Learning 课程指出,可以对 train 阶段每个 batch 计算的 mean/variance 采用指数加权平均来得到 test 阶段 mean/variance 的估计。
4. Batch Normalization 的优势
Batch Normalization 在实际工程中被证明了能够缓解神经网络难以训练的问题,BN 具有的有事可以总结为以下三点:
(1)BN使得网络中每层输入数据的分布相对稳定,加速模型学习速度
BN 通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内,使得后一层网络不必不断去适应底层网络中输入的变化,从而实现了网络中层与层之间的解耦,允许每一层进行独立学习,有利于提高整个神经网络的学习速度。
(2)BN使得模型对网络中的参数不那么敏感,简化调参过程,使得网络学习更加稳定
在神经网络中,我们经常会谨慎地采用一些权重初始化方法(例如 Xavier)或者合适的学习率来保证网络稳定训练。
当学习率设置太高时,会使得参数更新步伐过大,容易出现震荡和不收敛。但是使用 BN 的网络将不会受到参数数值大小的影响。例如,将参数 进行缩放得到
。对于缩放前的值
,设其均值为
,方差为
;对于缩放值
,设其均值为
,方差为
,则有:
,
忽略 ,则有:
注:公式中的
是当前层的输入,也是前一层的输出;不是下标!
可以看到,经过 BN 操作以后,权重的缩放值会被“抹去”,因此保证了输入数据分布稳定在一定范围内。另外,权重的缩放并不会影响到对 的梯度计算;并且当权重越大时,即
越大,
越小,意味着权重
的梯度反而越小,这样 BN 就保证了梯度不会依赖于参数的 scale,使得参数的更新处在更加稳定的状态。
因此,在使用 Batch Normalization 之后,抑制了参数微小变化随着网络层数加深被放大的问题,使得网络对参数大小的适应能力更强,此时我们可以设置较大的学习率而不用过于担心模型 divergence 的风险。
(3)BN 允许网络使用饱和性激活函数(例如 sigmoid,tanh等),缓解梯度消失问题
在不使用 BN 层的时候,由于网络的深度与复杂性,很容易使得底层网络变化累积到上层网络中,导致模型的训练很容易进入到激活函数的梯度饱和区;通过 normalize 操作可以让激活函数的输入数据落在梯度非饱和区,缓解梯度消失的问题;另外通过自适应学习 与
又让数据保留更多的原始信息。
(4)BN具有一定的正则化效果
在 Batch Normalization 中,由于使用 mini-batch 的均值与方差作为对整体训练样本均值与方差的估计,尽管每一个batch中的数据都是从总体样本中抽样得到,但不同 mini-batch 的均值与方差会有所不同,这就为网络的学习过程中增加了随机噪音,与 Dropout 通过关闭神经元给网络训练带来噪音类似,在一定程度上对模型起到了正则化的效果。
另外,原作者通过也证明了网络加入 BN 后,可以丢弃 Dropout,模型也同样具有很好的泛化效果。
5. 实验
现在通过实际的代码来对比加入 BN 前后的模型效果。使用 MNIST 数据集作为数据基础,并使用 TensorFlow 中的 Batch Normalization 结构来进行 BN 的实现。
BatchNorm 的本质思想
BN 的基本思想其实相当直观:因为深层神经网络在做非线性变换前的激活输入值(就是那个 ,
,U 是输入)随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近(对于 sigmoid 函数来说,意味着激活输入值  是大的负值或正值),所以这导致后向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因,而 BN 就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为
是大的负值或正值),所以这导致后向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因,而 BN 就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为 0 ,方差为 1 的标准正太分布而不是正态分布,其实就是把越来越偏的分布强制拉回比较标准的分布,这样使得激活输入值落在非线性函数对输入比较敏感的区域,这样输入的小变化就会导致损失函数较大的变化,意思是这样让梯度变大,避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。
其实一句话就是:对于每个隐层神经元,把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为 0,方差为 1 的比较标准的正态分布,使得非线性变换函数的输入值落入对输入比较敏感的区域,以此避免梯度消失问题。因为梯度一直都能保持比较大的状态,所以很明显对神经网络的参数调整效率比较高,就是变动大,就是说向损失函数最优值迈动的步子大,也就是说收敛地快。
Inception v3
源自论文 《Rethinking the Inception Architecture for Computer Vision》
1. 背景
自 ILSVRC2014 之后,GoogLeNet 备受追捧,它具有非常好的性能,虽然它的网络拓扑比较复杂,但是由于其特殊的设计模式,它的参数量、内存与计算资源的消耗都比传统的网络、甚至是同期的 VGG 相比,都要小很多,因此 GoogLeNet 的适用性更强。但是,GoogLeNet 也存在它的缺陷,Inception 的复杂性注定了网络的改变会很困难,随着网络结构的拓展,如果仅仅是简单的通过复制模块来对模型进行放大,模型计算上的优势将会消失,并且 GoogLeNet 原文中也并没有提出网络设计的原理和准则,因此很难在此基础上进行改变。
此论文文提供了一些通用的设计准则以及优化思路,并对 GoogLeNet 进行拓展,设计出了更加复杂、性能更好的 Inception v3 的结构。
2. 设计准则
- 避免特征表征的瓶颈(特征表征就是指图像在 CNN 某层的激活值,特征表征的大小在 CNN 中应该是缓慢的减小的,即 feature map 不应该出现急剧的衰减)。如果对流经层(尤其是卷积层)的信息过度的压缩,将会丢失大量的信息,对模型的训练也造成了困难。
- 在网络中对高维的表达进行局部的处理,将会使网络的训练增快。即高维的特征更容易处理,在高维特征上训练更快,更容易收敛。
- 在较低维度的输入上进行空间聚合,将不会造成任何表达能力上的损失,因为 feature map 上,临近区域上的表达具有很高的相关性,如果对输出进行空间聚合,那么将 feature map 的维度降低也不会减少表达的信息。这样的话,有利于信息的压缩,并加快了训练的速度。即低维嵌入空间上进行空间汇聚,损失并不是很大。这个的解释是相邻的神经单元之间具有很强的相关性,信息具有冗余。
- 设计网络的深度和宽度达到一个平衡的状态,要使得计算资源平衡的分配在模型的深度和宽度上面,才能最大化的提高模型的性能。即平衡网络的深度和宽度。宽度和深度适宜的话可以让网络应用到分布式上时具有比较平衡的 computational budget。
3. 改进方案(Factorizing Convolutions with Large Filter Size )
3.1 Factorization into smaller convolutions
考虑到第三条设计准则,由于 feature map 的临近区域具有很高的相关性,再使用空间聚合的前提下,可以减小 feature map 也就是 activation 的维度,因此也可以使用更小的滤波器(卷积)来提取局部的特征,同时这样做还可以提高计算的效率,例如将 7x7的 卷积替换成 3 个 3x3 卷积的叠加,将 5x5 的卷积替换成 2 个 3x3 卷积的叠加,这也是 VGG 所提到的改进。简而言之,就是将尺寸比较大的卷积,变成一系列 3×3 的卷积的叠加,这样既具有相同的视野,还具有更少的参数。

这样可能会有两个问题:
- 会不会降低表达能力?
3×3的卷积做了之后还需要再加激活函数么?(使用 ReLU 总是比没有要好)
实验表明,这样做不会导致性能的损失(在参数量和计算量上都减少了很多,多层的表达能力不会受到影响,同时增加了 ReLU,对模型的效果进行了改善。),于是Inception就可以进化了,变成了这样:

3.2 Spatial Factorization into Asymmetric Convolutions(不对称卷积)
作者又提出了一种非对称的方式,不仅减少了参数量,在计算量上又降低了 33%(使用 2 个 2×2 的话能节省 11% 的计算量,而使用这种方式则可以节省 33%)。 使用 3×3 的已经很小了,那么更小的 2×2 呢?2×2 虽然能使得参数进一步降低,但是不如另一种方式更加有效,那就是 Asymmetric 方式,即使用 1×3 和 3×1 两种来代替 3×3。于是,Inception再次进化:

实践证明,这种模式的 Inception 在前几层使用并不会导致好的效果,在 feature_map 的大小比较中等的时候使用会比较好,因此只有在 17x17 的 feature map 上才使用这种结构,其中 n=7。
3.2 Utility of Auxiliary Classifiers (辅助分类器)
在 GoogLeNet 中,使用了多余的在底层的分类器,直觉上可以认为这样做可以使底层能够在梯度下降中学的比较充分,但在实践中发现两条:
- 辅助的分类器在训练开始的时候并不能起到促进收敛作用,两者的效果是接近的,但在训练快结束的时候,使用辅助分类器的比没有使用辅助分类器的可以有所提升
- 最底层的那个多余的分类器去掉以后也不会有损失。
- 以为辅助分类器起到的是梯度传播下去的重要作用,但通过实验认为实际上起到的是 regularizer 的作用,因为在多余的分类器前添加 dropout 或者 batch normalization 后效果更佳。
在 GoogLeNet 的原始论文中提到了,在模型的中间层上使用了辅助的分类器,因为作者认为中间层的特征将有利于提高最终层的判别力。但是在这篇文章中,作者发现辅助层在训练初期并没有起到很好的效果,只有在增加了 BN 层或者 dropout 时,能够提升主分类器的性能。
3.3 Efficient Grid Size Reduction
Grid 就是图像在某一层的激活值,即 feature_map。一般情况下,如果想让图像缩小,可以有如下两种方式:

右图是正常的缩小,但计算量很大,需要 35x35x320x640x1x1 次乘法(不考虑 pooling 和加法,Kernel size:1x1)。而左图需要 17x17x320x640x1x1 次乘法。左图先 pooling 会导致特征表征遇到瓶颈,违反上面所说的第一个规则,为了同时达到不违反规则且降低计算量的作用,将网络改为下图:

使用两个并行化的模块可以降低计算量。右边的图从 feature map size 的角度展示的是同一种方法
为了避免第一条准则中提到的计算瓶颈所造成的的信息损失,一般会通过增加滤波器的数量来保持表达能力,但是计算量会增加。作者提出了一种并行的结构,使用两个并行的步长为 2 的模块,P 和 C。P 是一个池化层,C 是一个卷积层,然后将两个模型的响应组合到一起:

4. Inception v3 网络结构
经过上述各种Inception的进化,从而得到改进版的GoogLeNet,如下:

其中 figure5 为(没有进化的 Inception):

figure 6 为(smaller conv 版的 Inception):

figure 7 为(Asymmetric 版的 Inception):

5. Label Smoothing
除了上述的模型结构的改进以外,此篇论文还改进了目标函数。原来的目标函数,在单类情况下,如果某一类概率接近 1,其他的概率接近 0,那么会导致交叉熵取 log 后变得很大很大。从而导致两个问题:过拟合导致样本属于某个类别的概率非常的大,模型太过于自信自己的判断。所以,使用了一种平滑方法,可以使得类别概率之间的差别没有那么大:

用一个均匀分布做平滑,从而导致目标函数变为:

该项改动可以提升 0.2%。
6. Lower resolution input
这篇论文里还有关于低分辨率的输入的图像的处理,在图像分类和识别中,经常会遇到一个图片中的相对小 patch 的物体的检测和识别。比较有挑战的是这个 patch 很小而且低分辨率。一般来讲,输入的感受野分辨率越高,识别的效果越好,但同时网络模型会更大,计算量会更复杂。而如果我们只是改变了输入的分辨率而不要对模型做调整,为什么不用计算量更小的模型来解决识别分类问题。作者做了三个几乎相同计算量,高分辨率输入是否对检测结果影响的实验,如下图:

其中,
299x299的感受野:第一层后面接的是stride=2的卷积层和最大池化层151x151的感受野:第一层后面接的是stride=1的卷积层和最大池化层79x79的感受野:第一层后面接的是stride=1的卷积层,没有池化层。
训练是在 ILSVRC2012 数据集上进行训练,三个结果是差不多的。相同计算量下,高分辨率的输入对结果影响不是很大。这个结果也表明,R-CNN 中可以考虑使用专门的 high-cost 的低分辨率输入网络,来对小目标物体进行检测。
Inception v4(Inception-Resnet v1)
Resnet
1. 简介
源自论文 《Deep Residual Learning for Image Recognition》,是 MSRA 何恺明团队在 2015 年 ImageNet 上使用的网络,在当年的 classification、detection、localization 比赛中,ResNet 均获了第一名的好成绩。
2. 背景
2.1 深层网络的退化问题
首先作者提出了训练深度网络中发现的一个问题:在一定深度下,深层网络的训练误差大于浅层网络的训练误差。例如 56 层的网络训练误差大于 20 层的网络,如图所示:

如上图所示,作者做了一个对比实验,分别基于 CIFAR-10 数据集训练了一个 20 层和 56 层的网络。56 层网络的训练误差和测试误差都大于 20 层网络的训练误差,这显然不是过拟合导致的。这里的 “plain” networks 指的是由卷积、池化、全连接构成的传统的卷积神经网络,与 ResNet 不同。
2.2 问题分析
仔细分析可以得出:56 层的网络(下面称为 A 网络)不应该比 20 层网络(下面称为 B 网络)的训练误差大,因为把 A 网络看作是在 B 网络得结构基础上再添加 36 层得到的。那么可以将训练好的 A 网络分两部分考虑:
- 训练好的
A网络的前20层和B网络的训练结果完全相同 - 训练好的
A网络的后36层是对A网络的第20层输出做恒等映射,也就是不对A网络的第20层输出做改变。
如果优化器恰好可以将 A 网络参数训练为上述的情况,那么 A 网络的训练和测试误差应该与 B 网络相同。因此,可以推测实际训练的结果,应该是 A 网络的训练误差至少与 B 网络相同,不会更大。但是实验结果表明,A 网络的训练和测试误差比 B 网络的更大。这说明 A 网络在学习恒等映射的时候出了问题,也就是传统的网络(”plain” networks)很难去学习恒等映射(优化目标是让损失函数的值为 0,或者尽可能小,不是让残差等于 0)。
2.3 问题解决
假设 代表某个只包含有两三层的 block 的映射函数,
是 block 的输入,
是 block 的输出(假设它们具有相同的维度)。在训练的过程中,希望能够通过修改网络中的
和
去拟合一个理想的
(从输入到输出的一个理想的映射函数)。目标是修改
中的
和
来逼近
。如果改变思路,用
来逼近
,那么最终得到 block 的输出就由
变为
(这里的加指的是对应位置上的元素相加,也就是 element-wise addition),这里的直接将输入连接到输出的结构也称为 shortcut。
- 改变前目标: 训练
逼近
- 改变后目标:训练
逼近

如图所示,左边的是传统的 plain networks 的结构,右边的是修改为 ResNet 的结构。所谓的恒等映射就是输入 x 经过某一个函数(设为 G(x))作用输出还是 x 本身,即 G(x)=x。左边的 original block 需要调整其内部参数,使得输入的 x 经过卷积操作后,最终输出的 F(x) 等于 x,即实现了恒等映射 F(x)=x,等号左边是 block 的输出,右边是 block 的输入。但是这种结构的卷积网络很难调整其参数完美地实现 F(x)=x。再看右边的 ResNet,因为 shortcut 的引入,整个 block 的输出变成了 F(x)+x,block 的输入还是 x。此时网络需要调整其内部参数,使得 F(x)+x=x,也就是直接令其内部的所有参数为 0,使得 F(x)=0,F(x)+x=x 就变成了 0+x = x,等号左边是 block 的输出,右边是 block 的输入。输出等于输入,即完美地完成了恒等映射。
2.4 ResNet 结构为什么可以解决深度网络退化问题?
因为 ResNet 更加容易拟合恒等映射,而具体原因,回到刚才的问题分析部分,重新进行如下操作:
- 使用 ResNet 结构重新构建上述
A、B两个网络,A网络与B网络的前20层结构完全相同 - 训练
B网络得到各层参数 - 使
A网络与B网络的前20层参数完全相同(直接 copy 参数) A网络的后36层所有的参数置为0
可以看出,此时将 A 网络的输出误差应该与 B 网络相同(暂时不考虑网络中的维度大小的细节),因为 ResNet 结构的输出为 ,如果将网络中的参数置为
0,则 。因此得到的输出为:
,也就是恒等映射。这样就解决了上面提到的网络很难去拟合恒等映射的问题。因此使用 ResNet 结构搭建的深度网络至少与浅层网络具有相同的拟合能力,不会出现之前的网络退化问题。
但是 A 网络后面 36 层全部是恒等映射,这一定是此网络的最优解吗?答案显然是否定的,但是 ResNet 的结构使得网络具有与学习恒等映射的能力,同时也具有学习其他映射的能力。因此 ResNet 的结构要优于传统的卷积网络(plain networks)结构。

对比两种网络的训练和测试误差:

作者做实验对比了 plain-18、plain-34 和 Resnet-18、Resnet-34 之间的训练测试误差,结果如上图所示,Resnet-34 的训练和测试误差都小于 Resnet-18 的训练测试误差,这说明 Resnet 解决了网络的退化问题。
下面是作者搭建的其他深度的 Resnet 网络结构:

每个 block 的输入和输出的维度相等,因此在每个 block 内部 shortcut 直接与网络的输出相加,不同 block 的输入与输出的维度大小不同,因此需要进 行降采样使得 shortcut 的输出维度与网络输出维度相同才能进行相加,通常使用
1x1 的卷积核,stride=2 进行降采样,同时增加 feature map 的通道数。
2.5 Shortcut的三种方式
由于 ResNet 要求 与
的维度大小要一致才能够相加,因此在
与
维度不相同时,就需要对
的维度做调整,文章中提出了三种调整的方式:
- 如果
的维度增加,就使用
0来填充增加出来的维度(A 方式) - 如果
的维度增加,使用线性变换来增加多出来的维度,在程序里表现为使用一个
1x1的卷积核进行调整维度(B 方式) - 对于所有的 shortcut,都使用线性变换,也就是
1x1的卷积(C方式)
A 方式采用 0 填充.,完全不存在任何的残差学习能力。B 方式与 C 方式相比,错误率略高。但是 B 方式的模型复杂度要远低于 C 方式,因此,作者最终在所有的网络中采用方式 B。B 方式在 的维度与
的维度相同时,直接用
加上
,在
的维度与
的维度不同时,才采用
1x1 的卷积层对 的维度进行调整。
2.5 实验结果


作者搭建了不同深度的 ResNet 模型进行了实验,结果如上图所示。ResNet 在 ImageNet 上的错误率与网络的深度是线性关系,网络越深,错误率越低。说明在一定 ResNet 的网路结构解决之前所说的网络退化的问题。

这是作者在 CIFAR-10 上的实验结果,这里使用的 shortcut 是 A 方式,可以看出来在相同深度下,ResNet 的参数量远远小于其他网络,这也使得在训练和预测模型的时候计算比较快。作者还尝试训练了 1202 层的 ResNet,但是最终结果并没有 110 层的效果好,作者分析可能是因为过拟合的原因。作者还将 ResNet 用于 Faster-RCNN中,获得了 2015 年 COCO 的 detection 的冠军。
3. 原文翻译
Abstract
Deeper neural networks are more difficult to train. 我们提出了一个残差学习框架,目的是减轻更深的网络的训练。we explicitly reformulate the layers as learning residual functions with reference to the layer input, instead of learning unreferenced functions(直译为:我们将网络层的设计变为学习关于每层输入的残差函数—在数理统计中,残差是指实际观察值与估计值(拟合值)之间的差—而不是学习无参照函数)。我们提供了以实验为依据的证据,用以表明残差网络是更容易去最优化,并且可以从相当大的深度中获取精确度(一般的网络是这样的:随着网络深度的增加,训练精确度达到了饱和,然后再急剧衰退)。此外,深度残差网络相比较于 1/8 深 VGG 网络还更简单(网络越复杂,越容易过拟合)。
1. Introduction
深度卷积神经网络已经导致了关于图片分类领域一系列的突破。深度网络很自然的融合了低/中/高维度的特征,并且以一种端到端的多层方式进行分类,并且特征的“维度”可以通过堆积网络层得到丰富。最近的证据揭示了网络的深度是至关重要的;许多其他的有价值的视觉识别任务也非常得益于非常深的模型。
受深度这一重要性驱动,一个问题产生了:学习更好的网络是否像堆积更多的网络层一样简单。因为网络越深,越难学习—臭名昭著的梯度弥散或爆炸问题,其从一开始就阻碍(损失函数)收敛。然而,vanishing/exploding gradients 已经很大程度上得到了解决—受标准化的初始化及中间层的标准化(如中间层的标准化:batch normalization)—其使得具有数十层的网络得以用具备反向传递的随机梯度下降算法开始收敛。
当更深的网络可以开始收敛,一个衰退的问题被暴露出来:随着网络深度的增加,训练精确度达到了饱和,然后再急剧衰退。精度衰退并不是由过拟合导致的,而且为一个深度合适的模型增加更多的网络层会导致更高的训练错误(max-pooling layers result in loss of accurate spatial information (最大池化层会导致精确的空间信息的损失),这句话是 GoogLeNet 的作者说的;堆叠的多个非线性层不是恒等映射,所以作者此处通过恒等连接来近似拟合恒等映射)。在我的试验中得到了彻底的验证,如下图:

训练的精确性指明了:并不是所有的系统都相似的易于最优化。我们考量一个浅一点的架构以及在其浅层架构之上增加了更多网络层的更深的对应框架。存在一个对更深的模型进行构造的方式:增加的层是 identity mapping(恒等映射,即 f(x) = x,换句话说:输入为 x,在经历多个非线性网络层后输出仍是 x),而其他的网络层是从已学的浅层模型中复制。这种结构化的解决方案的存在指明了一个更深的模型应该产生比它更浅层的相对应模型更低的训练错误。但是实验表明,我们当前现有的求解程序无法找到好的或者比以上构造的方案更好的解决方案(意思是说,无法找到这样一种方案:输入为 x,在经历多个非线性网络层后输出仍是 x)。
在本文章中,我们通过引入一个深度残差学习框架来解决这个衰退的问题。我们明确的让这些网络层去拟合残差映射,而并没有期望每一堆叠层去直接拟合一个期望的潜在映射(拟合函数)。正式地,我们将期望的潜在映射指代为 H(x),让堆积的非线性层匹配其他的映射 F(x):H(x) - x,而最初的映射被重新投射为 F(x) + x。我们假设:相较于最优化最初的无参照映射(残差函数以输入 x 作为参照),最优化残差映射是更容易的。极限情况下,如果残差映射是最优化的,相较于通过一堆非线性层去拟合恒等映射,将残差逼近为 0 是更容易的(我们去最优化目标函数即最小化损失函数,通过链式法则,相当于将残差逼近为 0)。
F(x) + x 公式可以通过具有 shortcut connections 的前向传递神经网络得以实现,如下图:
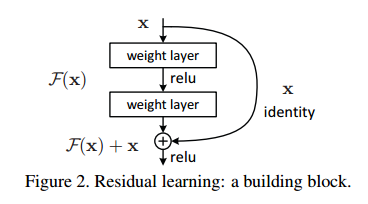
Shortcut connections 表示其跳过了一或多层。在我们的案例中,shortcut connections 仅仅执行 identity mapping,并且其输出与堆叠的网络层输出相加。恒等的 shortcut connections 连接既没有增加额外的参数又没有增加计算复杂度。整个网络任然可以通过具备反向传递的 SGD 算法进行端到端的训练,并且可以很容易的使用公共类库进行实现,而不需要修改求解程序。
我们在 ImageNet 上呈现了综合性的试验,用以表明衰退问题及评估我们的方法。我们得出了:1) 我们非常深的残差网络很容易最优化,但是当网络的深度加深时,与残差网络相对应的朴素网络(without shortcut connections)则表现了更高的训练错误;2) 我们的深度残差网络可以很容易的从急剧增加的深度中获得精确度,产生的结果大体上更好于先前的网络。如下图:

2. Related Work
Residual Representations(残差描绘)。在图片识别领域,VLAD(vector of locally aggregated descriptors)是一个描绘(将图片用向量进行表示),其通过关于一个字典的残差向量进行编码,Fisher Vector(characterize a signal with a gradient vector derived from a generative probability model and to subsequently feed this representation to a discriminative classifier,直译:用一个源自于一个生成式概率模型的梯度向量描绘一个信号,并且随后将这种描绘传递给一个可判别分类器 )可以公式化表示为 VLAD 的一个基于概率论的版本。两者都是关于图片检索及分类领域的强大的浅层描绘。对于向量的数字化,相较于编码原始向量,编码残差向量被证明是更有效率的。
In low-level vision and computer graphics,为了解决偏微分方程式(PDEs)的问题,广泛使用了 Multigrid(多表格)的方法去将系统重新表示为 subproblems at multiple scales(多尺度的子问题),其中每一个子问题由残差解决方案在一个更加粗糙及一个更加精细的尺度范围内负责。相对于 Multigrid 的一个另外的选择是 hierarchical basis preconditioning(分层的基础预处理),其依赖于在两个尺度之间进行表示的残差向量的变量。实验表明,相较于没有意识到解决方案残差属性的标准求解程序,这些求解程序收敛得更快。这些方法表明,一个优秀的重新公式化表述或预处理可以简化网络的优化。
Shortcut Connections。shortcut connections 的实践和理论已经研究了很长一段时间。一个训练多层感知器的早期实践是:加一个连接网络输入与输出的线性层。有人进行了这样的实验:把一些中间层直接连向附加的分类器,用以解决 vanishing/exploding gradients(梯度弥散/爆炸),如下图:
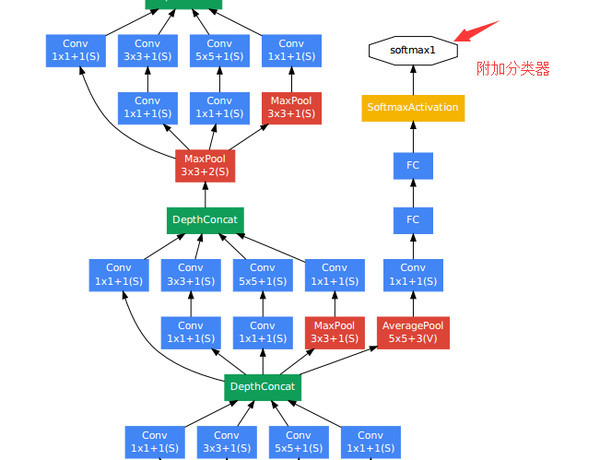
与我们的工作同时进行的,”highway networks”(公路网络)提出了 shortcut connection with gating functions(具有门控功能的捷径连接)。相较于我们没有参数的 identity shortcut,这些门是数据依赖的并且具有参数。当一个门控的 shortcut 是“关闭的”(接近于 0),公路网络层表示非残差函数。相反,我们的构想总是学习残差函数;我们的identity shortcut 从来不会关闭,并且所有的信息总是能够流过。
3. Deep Residual Learning
3.1. Residual Learning
我们将 H(x) 看作为用一些堆叠的网络层(不要求是整个网络)去拟合的潜在映射,x 指代为这几层的第一层的输入。If one hypothesizes that multiple nonlinear layers can asymptotically approximate complicated function,then it is equivalent to hypothesize that they can asymptotically approximate the residual functions,i.e.,H(x) - x(assuming that the input and the output are of the same dimensions)(存在这样一个假设:如果多个非线性层可以渐进地逼近复杂的函数,那么其相当于多个非线性层可以渐进地逼近复杂函数的残差函数:H(x) - x(假定输入和输出具有相同的维度))。所以,与其期望堆叠层去逼近 H(x),我们不如明确的让这些堆叠层去逼近一个残差函数 F(x):= H(x) - x。因此,最初的函数变为 F(x) + x。尽管两种形式都可以渐进地逼近预期的函数,但是学习的容易程度也许会不一样。
重新公式化表示(即 H(x) = F(x) + x)受关于衰退问题(朴素神经网络越深,训练错误越高)的违反自觉的现象所激励。正如我们在引言中讨论的,如果增加的网络层可以构造为 identity mappings,一个更深的网络模型应该具有比之更浅层的对应网络更低的训练错误。(训练精确性的)衰退问题表明,求解程序在通过多个非线性网络层去逼近恒等映射时也许会存在困难。由于残差学习的重新公式化表示,如果恒等映射是最优的,求解程序也许只要简单地将多个非线性网络层的权重向 0 逼近,以此逼近恒等映射(设 H(x) = F(x) + x,如果 F(x) = 0,那么 H(x) = F(x) + x = x 即为恒等映射;而 F(x) 等于权重 w 乘以输入 x 的复杂函数,如果要使得 F(x) = 0,那么权重 w 得为 0)。
在现实情况下,恒等映射是最优的是不太可能的,但是我们的重新公式化表示也许有助于预处理网络衰退的问题。If the optimal function is closer to an identity mapping than to a zero mapping, it should be easier for the solver to find the perturbation with reference to an identity mapping,than to learn the function as a new one(如果相较于接近一个 0 映射,最优化的函数更接近于一个恒等映射;那么对于求解程序来说,相较于像一个新的网络架构去学习目标函数那样,去发现关于恒等映射的扰动是更容易的)。我们通过实验表明了,通常来说,学习性的残差函数具有很小的响应,这表明恒等映射提供了一个令人满意的网络衰退的预处理。
3.2. Identity Mapping by Shortcuts
我对每几个堆叠网络层采用了残差学习。正式地,在本篇文章中, 我们仔细考虑将一个结构性模块定义为:
……(1)
其中,x 和 y 是网络层的输入和输出向量。函数代表需要学习的残差映射。对于 Figure 2 中具有两层网络的例子来说,
,其中,
指代为 ReLU 函数;此处为了简化概念,将偏置予以忽略。函数操作
是由一个 shortcut connection 和一个 element-wise addition 构成的。我们在加法之后采用了第二个非线性函数(即
)。
在上式中,x 和 F 的维度必须相同。如果不相同(例如,输入和输出的通道数量改变了),我们可以通过对残差连接执行一个权重为的线性的映射,用以匹配输入和输出的维度(该处的线性映射有点像 GoogLeNet 中的
1x1 的卷积,只不过在 GoogLeNet 中是用于 dimension reduction,而 ResNet 则是match dimension):
……(2)
我们也可以在式 (1) 中使用方阵(对于 fully-connected layer 来说,
是方阵;对于 convolution layer 来说,
是一个
4 维数组,例如其 shape[1, 1, in_channel, out_channel])。但是我们将会用实验表明:恒等映射足以解决网络衰退的问题,并且恒等映射是经济性的(introduce neither extra parameter nor computation complexity);因此只在需要匹配维度时才用。
残差函数 F 的形式是灵活的。本文中的实验涉及一个 具有 2 到 3 层的函数 F,尽管更多的层次也是有可能的。但是,如果函数F仅仅只有一层,则公式 (1) 类似于一个线性层:,而这并没有产生价值。
我们也指出:尽管以上的概念是为了简化概念而关于全连接层的,但是残差学习同样适用于卷积层。函数可以代表多个卷积层。
3.3. Network Architectures
Residual Network.
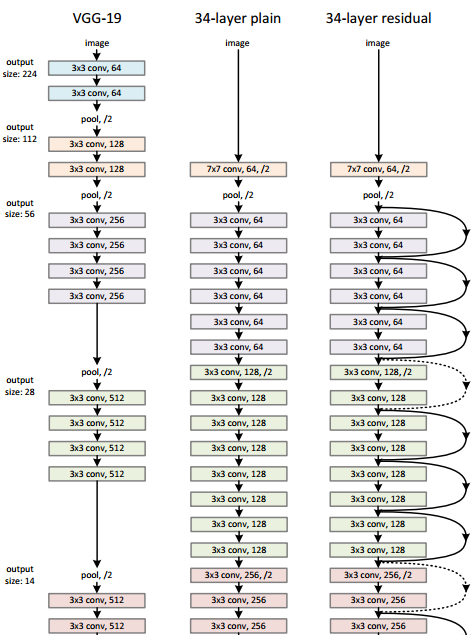
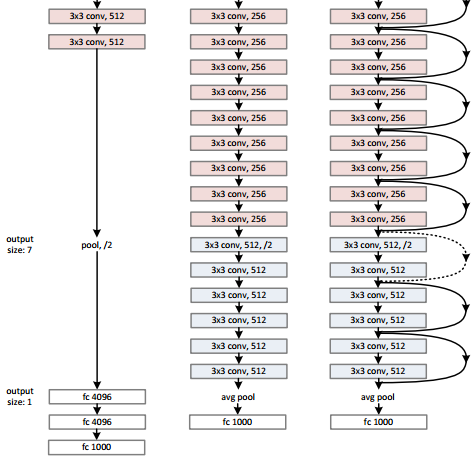
基于 plain network,我们插入了 shortcut connections (如上图所示),其将朴素网络转变为与其对应的残差版本。当输入和输出具有相同的维度,identity shortcut(即公式 (1))可以直接使用(如上图中实线 shortcut)。当维度增加时(上图中虚线shortcut),我们考虑了两种方案:
The shortcut still performs identity mapping,with extra zero entries padded for increasing dimensions. This option introduces no extra parameters(shortcut 仍然执行恒等映射,其具有额外的用于填补增加的维度的
0项,该选择没有增加额外的参数。The projection shortcut in Eqn.(2) is used to match dimensions(done by
1*1convolutions)(在公式 (2) 中的投影捷径用于匹配维度,可以通过1*1的卷积)。对于以上两种选择,when the shortcuts go across feature maps of two sizes, they are performed with a stride of2(当捷径跨越了两种大小的特征映射时,其执行的步长为2).
3.4. Implementation

图片的大小被重新度量:为了增加尺度,随机地在 [256, 480] 范围内进行取样,并用其较小边作为图片的大小。从一个图片中随机的取样一个大小为 224*224 的修剪块,或者对该修剪块进行水平翻转,并且每个像素减去其平均像素值。在进行卷积之后及 ReLU 之前,我们采用了 batch normalization(BN,可以加速训练,减少训练错误)。我们采用了一个大小为 256 的最小批处理 SGD。开始的学习速率为 0.1,并且当训练错误达到停滞时,学习速率在原先的基础上除以 10;此外,模型的训练迭代周期数为  。我们使用了一个
。我们使用了一个 0.0001 的权重衰退以及一个 0.9 的动量(即:,其中
为
0.9,为
0.0001,为
w 的范式)。但是我们并没有使用 dropout(用于控制过拟合的技术)。
4. Resnet TensorFlow 实现
为什么卷积层可以“代替”全连接层?
卷积和全连接的区别大致在于:
- 卷积是局部连接,计算局部信息
- 全连接是全局连接,计算全局信息(但二者都是采用的点积运算)
如果卷积核的 kernel_size 和输入 feature maps 的 size 一样,那么相当于该卷积核计算了全部 feature maps 的信息,则相当于是一个 kernel_size∗1 的全连接。
在全连接层上,相当于是 n∗m(其中,n 是输入的维度,m 是输出的维度)的全连接,其计算是通过一次导入到内存中计算完成;如果是在最后一个 feature maps 上展开后进行的全连接,这里若不进行展开,直接使用 output_size 的卷积核代替,则相当于是 n∗1 的全连接(这里的 n 就是 feature maps 展开的向量大小,也就是卷积核的大小 kernel_size∗kernel_size),使用 m 个卷积核,则可以相当于 n∗m 的全连接层。
但用卷积层代替全连接层的方式,其卷积核的计算是并行的,不需要同时读入内存中,所以使用卷积层的方式代替全连接层可以加开模型的优化。
为什么不能用卷积层代替全连接层的方式,使得模型处理不同大小的输入?
因为卷积层的运算是通过卷积核,说到底也就是点积运算,是需要事先设定参数的大小。 但如果这种操作用于处理不同 size 的输入,则实际上每次训练时,该层的参数 size 是不一样的,也就是模型不能得到训练。 虽然使用卷积层代替全连接层来处理不同大小输入的模型在整个流程上看起来没什么问题,但根本上,该模型是不能得到良好训练的(从代替的那层卷积层开始,其后的每一层得到的输入分布其实是一直在变化的,所以波动会比较大)。
全卷积神经网络Fully Convolutional Network (FCN)
全卷积神经网络即把 CNN 网络最后的全连接层替换为卷积,这样带来的好处:
卷积层和全连接层的区别:卷积层为局部连接;而全连接层则使用图像的全局信息。可以想象一下,最大的局部是不是就等于全局了?这首先说明全连接层使用卷积层来替代的可行性。
使用卷积层代替全连接层,可以让卷积网络在一张更大的输入图片上滑动,得到每个区域的输出(这样就突破了输入尺寸的限制)。解读如下:

DL 中的 GPU 和显存分析
1. 基础知识
nvidia-smi 是 Nvidia 显卡命令行管理套件,基于 NVML 库,旨在管理和监控 Nvidia GPU 设备(推荐一个好用的小工具:gpustat,直接 pip install gpustat即可安装,gpustat 基于 nvidia-smi,可以提供更美观简洁的展示,结合 watch 命令,可以动态实时监控 GPU 的使用情况。
watch --color -n1 gpustat -cpu
输出为:

显存可以看成是空间,类似于内存。
- 显存用于存放模型,数据
- 显存越大,所能运行的网络也就越大
GPU 计算单元类似于 CPU 中的核,用来进行数值计算。衡量计算量的单位是 flop: the number of floating-point multiplication-adds,浮点数先乘后加算一个 flop。计算能力越强大,速度越快。衡量计算能力的单位是 flops: 每秒能执行的 flop 数量:
1*2 + 3 1 flop
1*2 + 3*4 + 4*5 3 flop
2. 显存分析
2.1 存储指标
1 Byte = 8 bit
1 K = 1024 Byte
1 M = 1024 K
1 G = 1024 M
1 T = 1024 G
除了 K、M,G,T 等之外,常用的还有 KB 、MB,GB,TB 。二者有细微的差别。
1 Byte = 8 bit
1 KB = 1000 Byte
1 MB = 1000 KB
1 GB = 1000 MB
1 TB = 1000 GB
K、M,G,T 是以 1024 为底,而 KB 、MB,GB,TB 以 1000 为底。不过一般来说,在估算显存大小的时候,不需要严格的区分这二者。对于 OEM 厂商,在进行硬盘的设计时,便采用的是第二种方式,所以这就是为什么标注 512G 容量实际上只有大约 476G 左右的原因。
常用的数值类型如下图所示( int64 准确的说应该是对应 C 中的 long long 类型,long 类型在 32 位机器上等效于 int32):

其中,float32 是在深度学习中最常用的数值类型,称为单精度浮点数,每一个单精度浮点数占用4 Byte 的显存。
举例来说:有一个 1000x1000 的矩阵,float32 类型,那么占用的显存差不多就是:
1000 x 1000 x 4 Byte = 4 MB
32x3x256x256 的四维数组(BxCxHxW)占用显存为:24 M
2.2 神经网络显存占用
神经网络模型占用的显存包括:
- 模型自身的参数
- 模型的输出
举例来说,对于如下图所示的一个全连接网络(不考虑偏置项 b):

模型的显存占用包括:
- 参数:二维数组
w - 模型的输出: 二维数组
y
输入 X 可以看成是上一层的输出,因此把它的显存占用归于上一层。这么看来显存占用就是 w 和 y 两个数组?并非如此!!!
2.2.1 参数的显存占用
只有有参数的层,才会有显存占用。这部份的显存占用和输入无关,模型加载完成之后就会占用,主要包括:
有参数的层主要包括:
- 卷积
- 全连接
- BatchNorm
- Embedding层
- … …
无参数的层:
- 多数的激活层(Sigmoid/ReLU)
- 池化层
- Dropout
- … …
更具体的来说,模型的参数数目(这里均不考虑偏置项 b)为:
Linear(M->N):参数数目:M×NConv2d(Cin, Cout, K):参数数目:Cin × Cout × K × KBatchNorm(N):参数数目:2NEmbedding(N,W):参数数目:N × W
参数占用显存 = 参数数目 × n
n = 4:float32n = 2:float16n = 8:double64
在 PyTorch 中,当执行完 model=MyGreatModel().cuda() 之后就会占用相应的显存,占用的显存大小基本与上述分析的显存差不多(会稍大一些,因为还有其它开销)。
2.2.2 梯度与动量的显存占用
举例来说, 优化器如果是 SGD:

可以看出来,除了保存 w 之外还要保存对应的梯度  。因此,
。因此,显存占用 = 参数占用的显存 x 2。
如果是带 Momentum-SGD

这时候还需要保存动量, 因此,显存 x 3。如果是 Adam 优化器,动量占用的显存更多,显存 x 4。
总结一下,模型中与输入无关的显存占用包括:
- 参数
w - 梯度
dw(一般与参数一样) - 优化器的动量(普通 SGD 没有动量,momentum-SGD 动量与梯度一样,Adam 优化器动量的数量是梯度的两倍)
2.2.3 输入输出的显存占用
这部份的显存主要看输出的 feature map 的形状。
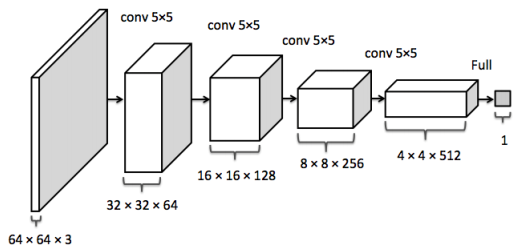
比如卷积的输入输出满足以下关系:
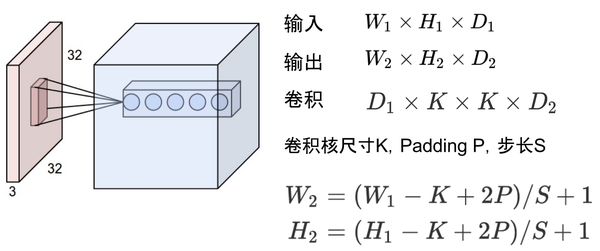
据此可以计算出每一层输出的 Tensor 的形状,然后就能计算出相应的显存占用。
模型输出的显存占用,总结如下:
- 需要计算每一层的 feature map 的形状(多维数组的形状)
- 需要保存输出对应的梯度用以反向传播(链式法则)
- 显存占用与 batch size 成正比
- 模型输出不需要存储相应的动量信息。
深度学习中神经网络的显存占用,可以得到如下公式:
显存占用 = 模型显存占用 + batch_size × 每个样本的显存占用
可以看出显存不是和 batch-size 简单的成正比,尤其是模型自身比较复杂的情况下:比如全连接很大,Embedding 层很大。
另外需要注意:
- 输入(数据,图片)一般不需要计算梯度
- 神经网络的每一层输入输出都需要保存下来,用来反向传播,但是在某些特殊的情况下,我们可以不要保存输入。比如 ReLU,在 PyTorch 中,使用
nn.ReLU(inplace = True)能将激活函数 ReLU 的输出直接覆盖保存于模型的输入之中,节省不少显存(y=relu(x) -> dx = dy.copy(); dx[y<=0]=0)。
2.3 节约显存的方法
在深度学习中,一般占用显存最多的是卷积等层的输出,模型参数占用的显存相对较少,而且不太好优化。
节省显存一般有如下方法:
- 降低 batch-size
- 下采样(
NCHW -> (1/4)*NCHW) - 减少全连接层(一般只留最后一层分类用的全连接层)
3. 计算量分析
计算量越大,操作越费时,运行神经网络花费的时间越多。
3.1 常用操作的计算量
常用的操作计算量如下:
全连接层:
BxMxN,B是 batch size,M是输入形状,N是输出形状。
卷积的计算量:

BatchNorm:计算量估算大概是
池化的计算量:

ReLU 的计算量:
BHWC
3.2 AlexNet 的显存占用
AlexNet 的分析如下图,左边是每一层的参数数目(不是显存占用),右边是消耗的计算资源. 这里某些地方的计算结果可能和上面的公式对不上,这是因为原始的 AlexNet 实现有点特殊(在多块 GPU 上实现的)。

可以看出:
- 全连接层占据了绝大多数的参数
- 卷积层的计算量最大
3.3 减少卷积层的计算量
谷歌提出的 MobileNet 利用了一种被称为 DepthWise Convolution 的技术,将神经网络运行速度提升许多,它的核心思想就是:把一个卷积操作拆分成两个相对简单的操作的组合。如图所示, 左边是原始卷积操作,右边是两个特殊而又简单的卷积操作的组合(上面类似于池化的操作,但是有权重,下面类似于全连接操作)。

这种操作使得:
- 显存占用变多(每一步的输出都要保存)
- 计算量变少了许多,变成原来的(
)(一般为原来的
10-15%)
3.4 常用模型的比较(显存/计算复杂度/准确率)
论文《AN ANALYSIS OF DEEP NEURAL NETWORK MODELS
FOR PRACTICAL APPLICATIONS》总结了当时常用模型的各项指标,横座标是计算复杂度(越往右越慢,越耗时),纵座标是准确率(越高越好),圆的面积是参数数量(不是显存占用),参数量越多,保存的模型文件越大。左上角我画了一个红色小圆,那是最理想的模型:快,准确率高,显存占用小。

4. 总结
4.1 建议
- 时间更宝贵,尽可能使模型变快(减少
flop) - 显存占用不是和 batch size 简单成正比,模型自身的参数及其延伸出来的数据也要占据显存
- batch size 越大,速度未必越快。在你充分利用计算资源的时候,加大 batch size 在速度上的提升很有限
尤其是 batch-size,假定 GPU 处理单元已经充分利用的情况下:
- 增大 batch size 能增大速度,但是很有限(主要是并行计算的优化)
- 增大 batch size 能减缓梯度震荡,需要更少的迭代优化次数,收敛的更快,但是每次迭代耗时更长。
- 增大 batch size 使得一个 epoch 所能进行的优化次数变少,收敛可能变慢,从而需要更多时间才能收敛(比如 batch_size 变成全部样本数目)。
4.2 显卡的选购
市面上常用的显卡指标如下(Base Core,不考虑 TensorCore 和 Boost 等)):

显然 GTX 1080TI 性价比最高,速度超越 Titan X,价格却便宜很多,显存也只少了 1G。
- K80 性价比很低(速度慢,贵)
- 注意 GTX TITAN X 和 Nvidia TITAN X 的区别
- TensorCore 的性能目前来看还无法全面发挥出来,这里不考虑。其它的 tesla 系列像 P100 这些企业级的显卡普通消费者不会买,而且性价比较低